 PR
PR2026.02.26
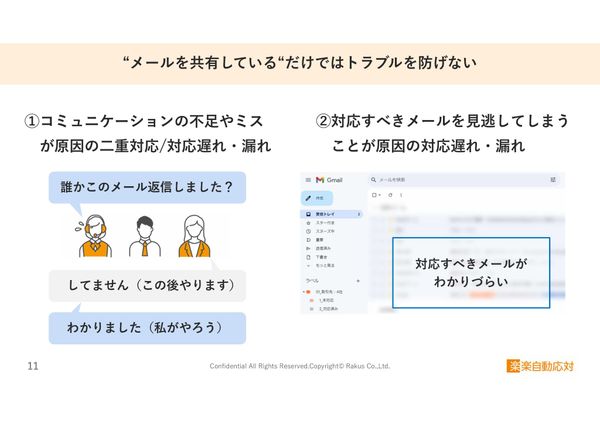
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
ゼータの普遍性 ~ゼータの持つ驚くべき性質~(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
司会者:前回、飛び込みプレゼンでしたが、その飛び込みプレゼンがあまりにもすばらしかったので今回はゲストプレゼンターとして登場していただきます。
ご紹介しましょう、せきゅーんさん、お願いいたします。
(会場拍手)
せきゅーん:では、今日はリーマンゼータ関数の話をします。
なにがロマンティックかといいますと、まず値がロマンティックで、偶数における値は円周率がなぜかでてくる。奇数における値は、なにもわかっていないんですけれども、(ζ(3)が)無理数であることが証明されている。これだけわかっています。

すごくロマンティックなのが、素数と結びついているんです。 すべての素数pが協力することによって1つの関数になっている。

すごいですねぇ。
(会場笑)
リーマンはこれを複素平面全体に解析接続しまして、実部が1/2の直線上で対称性を持つという非常に美しい関数等式を証明しました。
このように全平面で定義されたリーマンゼータ関数に複素解析関数論を応用することによってx以下の素数の個数が約 x/logx である素数定理や、それがきっちりこのように、こんなに簡単な式で書ける!

(会場笑)
リーマン素数公式などそもそも、ρは、つまり素数の公式はないと言われますが、あります。
ただ、このρというのはリーマンゼータ関数の非自明な零点で、この点が非常に難しく、さらに実部がすべて1/2であるというのが、100万ドルの懸賞金がかけられているリーマン予想なわけです。

この1/2のラインをクリティカルラインと言いまして、この幅の部分をクリティカルストリップと言います。

この緑の部分が自明な零点と言われていて、クリティカルストリップ以外には、緑の分しかないということが簡単にわかるんですけれども、この幅の部分にある零点というのは全部この一直線上に並んでいるだろうというのが、リーマン予想でしたね、はい。
(会場笑)
それは知っていると思うので今日はゼータの、超ロマンティックな性質を1つ覚えて帰っていただきます。 ロマンティックゼータナイト。
(会場笑)
その前に復習しましょう。知らなくても復習します。
閉区間[a,b]上定義された任意の連続関数f(x)を考える、このとき、任意の ε>0 に対して、そのεの精度で、ある多項式P(x) はεごとに存在して、多項式で近似できますよね?
(会場笑)

これの複素版がありまして、メルゲリアンの多項式近似定理っていうのは複素版で、だいたい閉区間というのが、複素平面Cにおける補集合は連結であるようなコンパクト集合にして連続を正則にしたような感じ?
(会場笑)
復習は終わりです。
本日のロマンティックスーパーヒーローはセルゲイ・ボローニン。

(スライドを指して)Wikipedia引用です。彼は1975年、とんでもない定理を証明しました。
まず、リーマンゼータというのは、リーマン予想が大変なので、その1/2を真ん中にする0,1の間の区間を知りたいんですけども対称性があるんですよね、関数等式で。

だから、右側を考えましょう。その右側の中の補集合が連結であるようなコンパクト集合Kを取ったときにそのK上連続関数non-zero、これが重要、零点なくて、Kの内部で正則であると仮定する任意の関数f(x)をとりましょう。このとき、まことに驚くべきことに、リーマンゼータ関数をこの虚部をスライドさせることによってf(s)に任意の精度で近似できるようなτが必ず存在して、しかもその密度が、ゼロより大きい。だから、え、これやばくないですか!?
(会場笑)
すなわち、K上定義された零点を持たない任意の解析関数は、リーマンゼータ関数というたった1つの関数で近似できるんですよ。先ほどの定理は、多項式と言っても、関数の種類ですからたくさんあるわけですよね。でもこれ、たった1つのリーマンゼータ関数がすべての関数を近似できると言っているんですよ、なんてことだ!
(会場笑)
リーマンゼータ関数というのは、K上、零ではないすべての解析関数の情報を有しているといえる。幅は短いじゃんと思うかもしれないけれど、平行移動や縮小などをすればどんな関数でも考えられるわけで、ちょっとこの関数のこの部分の形、この精度で近似してと言われても、リーマンゼータただ1つでスライドすれば、無限にたくさん複製できるんですよ。
これは解析関数界の万能細胞です。
(会場笑)
証明は難しいです。個人的におもしろいのは、Riemann's Rearrangement Theorem のヒルベルト空間への一般化を応用する部分。
(会場笑)
あれですよ、Rearrangement Theoremって、収束が条件収束であるような級数って並び替えたらどんな値にでもできるってやつ、あれを応用するんですよ、かっこよくないですか?
(会場笑)
それでは応用を述べましょう。このσをクリティカルストリップ内の点、固定したときに、微分の並べたやつというのはCのn乗の中で稠密なんですよね。これを使うとですね、驚くべきことにリーマンゼータというのは、一切、微分方程式を満たしません。やばくないですか?
しかもこれ、このF(s) の部分を多項式に限定したときに、代数的微分方程式って言うんですけど、これをを満たさないことはヒルベルトも予想もしてましたが、F(s) が任意の連続関数であっても微分方程式を満たさないんですよね。……やばい!
(会場笑)
では最後です。リーマン予想との関係を述べましょう。先ほど、このボローニンの普遍性定理というのは零点を持たないという情報が重要でした。しかしリーマン予想が解けていない以上、リーマンゼータそれ自身は近似できるかわからないわけですね。
しかし、まことに驚くべきことに、リーマンゼータそれ自身をリーマンゼータが近似できるならば、リーマン予想は成り立つ、逆も成り立つんです。
すなわちですよ、リーマンゼータというのは万能細胞だったわけですが、自分自身をも近似できる、ある種の自己言及性が成り立つということこそがリーマン予想だったんです!
(会場拍手)
すばらしい。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします