 PR
PR2026.01.19
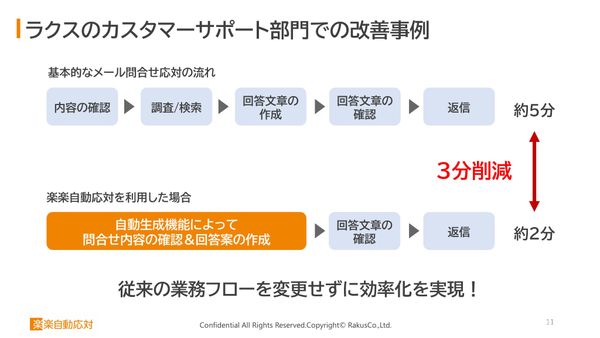
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
The Fibonacci Sequence: Nature's Code(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
ハンク・グリーン氏:数学というものは、アメリカの大学生をいじめるために考案されたのではありません。自然界におけるちょっとした事柄、身の回りのあちこちで目にするものなのです。
例えば実際に、自然界にいつでも見られる特別な数列、「フィボナッチ数列」と呼ばれる一連の数があります。
1、1、2、3、5、8、13、21、34、55、というふうに続いていく数列ですね。
もしかしたらこのパターンに見覚えがあるかもしれません。
最初の数字と2番目の数字が足しあわされて3番目の数字になり、2番目の数字と3番目の数字が足しあわされて4番目の数字になり、4番目の数字と5番目の数字が足しあわされて6番目の数字になる、という具合に続いていきます。
この数列は1,300年ほど前に、インドの数学者が書物に記しました。
西欧社会に姿を見せたのは1202年にピサのレオナルド、通称フィボナッチがその書物を紹介してからです。
こうしてアラビア数字がヨーロッパに導入されなければ、私たちは今でもローマ数字を使っていたかもしれません。考えただけでぞっとしますね。
数学者だったフィボナッチは、自著『算盤の書』のなかで、近親相姦を行っていくウサギたちを例にとってフィボナッチ数列を説明しています。
オス・メス1匹ずつをつがいにすれば2匹です。2匹が子供を産んで3匹になり、その3匹で子供を産めば5匹になっていく……そういった内容です。
しかし、フィボナッチ数が自然界において顕著に見られるのは、ウサギではなく植物なのです。
バナナを切ってその断面を見ると、3つの領域に分かれています。

リンゴなら5つです。

どんな花であったとしてもその花びらは、3、5、8、13、21枚になっています。



ヒマワリの種や松ぼっくりのかさの並びにもフィボナッチ数列が潜んでいます。


植物たちはなにか神秘的な、意思がはたらいたようにこの法則に則って成長するのです。
これによって、限られたスペースにできるだけ多くの種をしまえるのです。この話を詳しく知りたい人は、Vi Hartのビデオをごらんください。(YouTubeの)概要欄にリンクを貼っておきますね。
フィボナッチ数そのものだけではなく、フォボナッチ数同士の比率も潜んでいます。
適当なフィボナッチ数をその1つ前の数字を割ってみると、とくに大きな数字であれば、1.618……とどこまでも続いていく値が得られます。
フィボナッチよりはるか昔のギリシャでは、これを「ファイ」とよんでいました。今日では、「黄金比」としても知られています。
伝承によると、古代ギリシャの彫刻家ペイディアスが、肉体の成熟さを表現するために用いたとされています。
例えば、彫刻全体の身長と、足からへそまでの長さの比に用いたと言われています。ほかにも顔の長さを幅で割った値もそうです。
自然界にはこうしたパターンがほかにも数多く見られますが、そのなかには「黄金長方形」に基づくものもあります。
黄金長方形とは、フィボナッチ数の連続した数字、例えば8×13のような数字が辺の長さになっている長方形のことです。
黄金長方形は連続した数字の長方形を埋め込んでいくことができます。1×1、2×2、3×3、5×5、8×8といった具合ですね。

各正方形の対角同士で弧を描いて得られるらせんは、自然界に数多く見られるらせんとよく似ています。砂漠の多肉植物が葉を開いた様子、松ぼっくりのかさの並び方、ヒマワリの種、オウムガイの殻。



数学というものは、本当に美しいですね。
 Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル
Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします