 PR
PR2026.02.26
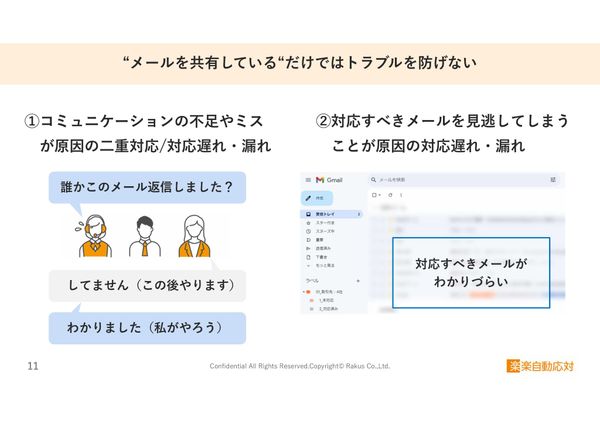
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
RPGで数列(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏(以下、安原):パート5は、かなり具体的な例を出してみようかなと思います。(スライドを示して)RPGは、ロールプレイングゲームのつもりで書いています。「RPGで数列」という話をしてみましょう。

自分がレベル5のプレイヤーだったとしましょう。ロールプレイングゲームは、見えていない場合もありますが、だいたい敵にもレベルがあります。
自分よりもレベルが低い敵には楽勝で、同じレベルの敵はいい勝負。そして、1つ上のレベルはちょっと厳しいというゲームデザインをするでしょう。このように作っていくものだと思います。こういう状況で、適切な経験値をどう与えたらいいのかという話をしてみましょう。

順番に考えてみましょう。レベルアップ条件。例えば自分と同じレベルの敵、つまり自分がレベル5であれば、レベル5の敵を5体倒すと1レベル上がるとしましょう。

この時、低いレベルの敵は5体では困りますよね。もっと数が多くあってほしいわけです。つまりそいつら(低いレベルの敵)には楽勝なので、面倒くさくあってほしいわけです。なので、低いレベルの敵は8体倒さなきゃいけない。でも8体倒せばレベルアップします。
逆に、自分より1つ高いレベルの敵は、3体倒すだけでレベルアップするというゲームデザインをわりと考えていきたいのではないでしょうか。

仕事としては、プランナーさんの仕事になるかとは思いますが、この時に数列や数学を使えないと企画がちゃんとできないので、心して聞いてもらいたいと思います。
もう1つ大事なことがあります。レベル5からレベル6にいく時と、レベル31まで上り詰めてレベル32にいく時は、やはり同じぐらいのレベルの敵5体でレベルアップしたいんですね。

そうじゃないと、1日遊んでもレベルアップしないというつらいことが起きてしまいます。やはりレベルアップの頻度は変えたくないので、こういう要件も必要です。
ここでは敵ごとに得られる経験値があるとして、それを固定にしましょう。例えば自分のレベルがいくつであってもレベル4の敵を倒したら経験値は、いくつ。この値を自分のレベルには関係なく固定したいと思ったとしましょう。
このような条件で考えていくと、そんなに複雑ではないと思います。(スライドの)左上のところを見てください。レベル1からレベル2にいくのに、10と書いてありますね。10の経験値をゲットすると、レベル2になれるとしましょう。ではレベル3になるにはいくつ必要かというと、10では困るわけですね。これを1.5倍して、15の経験値を稼ぐとレベル3になるようにしようと設計していくのが1つの例かなと思います。
この1.5倍をずっと守り続けるわけです。そうすると、レベル31という“つよつよ”状態でも、レベル31から32になるためには、191万7,511の経験値が必要で、その次は287万必要です。

これは、等比数列と呼ばれる数列の種類です。初項が10で、公比は1.5になります。この等比数列を解けるようにしましょうという話ですね。
そんなに難しくはないと思います。学校でもやっていると思いますし、復習してもそんなに手間はかからないんじゃないですかね。10、15とあって、結局1.5のn-1乗というのがレベルnです。スモールnのほうですね。

10掛ける1.5のn-1乗で、レベルアップに必要な経験値を計算できます。これを文字に置き換えて、初項がIだとすると、公比aがあって、Iのa乗マイナス1となります。

これで、ネクスト経験値を計算できちゃいます。かなり単純ですね。もっと複雑にしたい場合もあると思いますが、これが基本です。
少しだけ応用を考えていきます。白い四角で0、10、25と上に書いてあるのを見てください。ごめんなさい、ちょっと数字が間違っていますね。(青字の)100と書いたのは10で、150のところは15です。
累積経験値がこの白い四角の中に入っています。例えばレベル32になった人は、経験値を固定の値で持っていて、その値は等比数列の和である必要があります。

これは数列の授業で習った等比数列の和の公式です。Mn(※nは下付き文字)イコールシグマがあって、ちょっと「うえっ」となるんですが、シグマ、このZみたいな文字はぜんぜんなんてことはありません。みなさんがふだん書いているforループと同じです。
for、k=1で、「kがnより小さい間ループしなさいよ」で、その中にあるaのk-1乗を1個ずつ足していきましょうという数式にほかならないわけです。なので、プログラムを書いたことがある人だったら、このシグマという文字を恐れる必要はぜんぜんありません。
ただ、ループじゃないと解けないのは困るので、(スライドを示して)一番右の公式があるわけです。これで累積値は一発で出せます。一般項が出せるわけです。

というわけで、ぜひ「Excel」の表に式を入れてダーッと見てほしいのですが、レベル40ぐらいになるとけっこう大きな値になっています。
なので、これが32ビットで収まるかも同時に検討しておく必要があります。ゲームを作っている途中で「やはりダメだった」となると、プログラマーさんにかなり怒られますよね。きちんと式を知っていれば、こういうのもあらかじめわかります。

もう1回このスライドを出しました。一番右下に書いてある公式、ちょっと嫌じゃないですか。「知らんがな」「覚えていられないよ」と思うかもしれませんが、実は僕、この公式を覚えているんですね。覚え方があるので、おまけとしてその話をしましょう。

xの2乗マイナス1という式を見た時、こう因数分解をしたくなるじゃないですか。x-1とx+1を掛けたのがxの2乗マイナス1という式があります。
これには実は応用があって、3乗引く1だとか、4乗引く1だとか、「なんとか乗引く1」だったら、必ずx-1で割れます。残った数が、おもしろいことに階段状になっている。「xの3乗プラス、xの2乗プラス、xプラス1」みたいになっているので、xのn乗引く1というのがあっても、必ずx-1で割り切れて、残りは階段状になる性質があります。


こういう式をもう1回出しました。等式をいじるだけ、つまり両辺をx-1で割るだけで、先ほど見たような式が出てきます。(スライドを示して)一番右下のところを見てください。xのn乗マイナス1、この黄緑で書いた部分を見ると、「これx-1で割り切れるじゃん」と思うじゃないですか。割った残りは、n-1の階段状の足し算になっている、つまりこのシグマの値と一致しているということになるので、そう考えると先ほどの式もそんなに難しくはないかなと思います。

もう1つ、おまけっぽい話をします。(スライドを示して)こういうふうに経験値の累積があったとしましょう。今このプレイヤーは、100万の経験値を持っている。逆算してプレイヤーが今何レベルなのかを計算をする羽目になるかもしれません。それも計算できるようになっておこうねという話です。

これは、nイコールに直せばよくて、これが答えです。下から2番目で、aのn乗イコールという式になりますが、ここからは対数を知らないと解けません。対数がわかっていれば、最後の式までたどり着けます。なので、対数はやはり大事かなと思います。

レベルと経験値は完全に一致します。経験値があればレベルはわかるので、例えば「セーブデータに格納する時は、レベルの値を入れる必要ないよね」という議論だってできます。
というわけで、パート5のまとめです。経験値は、指数関数で実装できるんじゃないかなと思います。僕はロールプレイングゲームを作ったことがないので、実際のところは知りませんが、たぶんこういう感じで作っていて、少なくとも今回のお話に矛盾はないと思います。
等比数列はけっこう大事でよく出てくるので、使えるようになっておきましょうという話ですね。
それから、対数があれば経験値からレベルを逆算できます。ここもそんなに難しい内容ではありませんが、ブログを書いたので、あとで参照してもらえればよいかなと思います。

というわけでパート5は以上でした。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします