 PR
PR2026.02.26
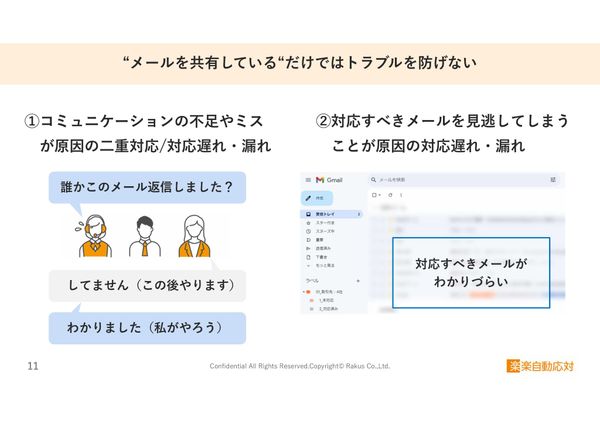
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
SHAP(SHapley Additive exPlanations)で機械学習モデルを解釈する(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
森下光之助 氏(以下、森下):まずは簡単に自己紹介をさせてください。僕はTVISION INSIGHTS株式会社でデータサイエンティストのマネージャーをやっていて、僕自身もテレビの視聴行動を分析しています。弊社ではセンサーを各家庭に置かせてもらって、個人が「テレビの前にいます」とか「目がテレビに向いてます」といったデータを取得し、テレビマーケティングのための分析を行なっています。
今日はSHapley Additive exPlanations(以下、SHAP)についてご紹介させていただければと思っています。よく「機械学習モデルを協力ゲーム理論を使ってうまいこと解釈できます」みたいなことが書いてありますよね。「なるほど」と思うところもあったんですけど、よくわからなかったので勉強しました。
まずは、モチベーションなんですけど、予測を解釈する文脈でどういうことが問題になっていて、それをSHAPがどういうふうに解決するのかをお話しします。
解釈性の文脈では「予測値に理由付けがほしい」ということがよく言われます。例えば、(機械学習モデルを使って)ローンの審査をするときに、ブラックボックスモデルを使って予測をするとします。そうすると理由は分からないけど、「この人はローンの返済確率が低いのでローンを貸し出せません」という結果が出たりします。当然なぜ「ローンの返済確率が低い」と予測されたかの説明が求められます。
似たような文脈で、例えば、病気になる確率が高いという結果が出たときに、なぜ病気になる確率が高いと出たのか説明する必要が出てきます。病気になる確率が高い原因は食生活によるものなのか、あるいは運動不足によるものなのか。それがわかると改善するための施策を打てばいいよねみたいな話になる感じですね。
もう少し一般的に言うと、特徴量がM個の学習モデルを考えてみます。(モデルの)平均的な予測値とあるインスタンスの予測値があるときに、その差分を各特徴量の貢献度に分解できるのではないかというのが基本的なアイディアです。
このような貢献度による分解をAdditive Feature Attribution Methodと呼んでいます。足し算のかたちで表現できるということですね。これはどういうことかを、年収予測の例で考えます。ある個人の年収は1,000万円と予測されました。平均的な予測は500万円だったとします。
ここで差分の500万円は何が原因で生じているのかというのを考えます。「学歴が修士」(+200万円)、「専門はCS(コンピューター・サイエンス)」(+300万円)、「役職は課長」(+300万円)、だから(+700万円の価値のある)良いデータサイエンティストという評価になるんですけど、「英語が話せない」ので少し低め(−200万円)にしておきましょうみたいな感じですね。
やりたいことはわかるんですけど、どうやって計算するかということですよね。線形モデルの場合は簡単に分解できそうで、(スライドの)一番下みたいな感じに式が変形できて、それぞれの「変数の係数」×「期待値からどのくらい変数が乖離しているのか」で貢献度が分解できます。
線形モデルだと簡単にみえるんですけど、モデルが複雑だとどう分解すればいいのかが明らかではないですよね。これを協力ゲーム理論のShapley Valueで説明しようというのがSHAPの考え方になります。
なので、協力ゲーム理論とShapley Valueについて見ていきます。
全体を語ると訳がわからなくなるので、ここではアルバイトゲームという具体的な例について考えてみます。A君、B君、C君の3人がいて、アルバイトをします。誰が参加するかによって報酬が変わるということを考えます。
3人全員が働くと報酬が24万円もらえるんですけど、この24万円の報酬をどのように配分するのがフェアなのかという問題を考えていきます。フェアな配分というのは、単に8万円ずつ山分けするとかもあると思うんですけど、貢献度がより高い人により多くの分配をするのもある意味でフェアなので、今回はそういう配分を考えます。
※参考文献『ゲーム理論 新版』
ここで貢献度をどうやって計るのかという話になりますよね。このために限界貢献度という概念を導入します。限界貢献度は、例えばA君の場合は、A君がアルバイトに参加したとき、報酬がどのくらい増えるのかをもって限界的な貢献度とすると定義します。
まず、誰もいないところからA君が参加すると報酬は0から6万円になります。+6万円ですね。次にB君が参加表明しているところにA君も参加すると+16万円になります。そして、C君が参加しますというところにA君が参加すると、これは+13万円になります。こんな感じでA君が参加したときに報酬がどのくらい増えるのかというのは、既に誰が参加表明しているかの順番に依存するということが起きます。
この順番の効果を打ち消したいので、すべての順番に関して限界貢献度というのを求めて、それの平均を取ります。こうやって求めた平均的な限界貢献度のことをShapley Valueと呼びます。このShapley Valueを用いて報酬を配分すると、ある意味でもっともらしい配分のひとつになっているということが数学的に示されています。
例えば貢献度が高い人に、より多くの報酬が渡されるなど望ましい性質を持っていて、さらに一人ひとりのShapley Valueの値を全部足すと24万円になって余りなく配分できるという性質もあります。
今は3人のゲームについて話をしたんですけど、これは一般的なM人のゲームにも拡張できます。やっていることは単純で、結局プレイヤーjというのが参加したときと参加していないときの差分というのが限界貢献度になるので、それをすべての順番について求めて平均するということをやってます。これが協力ゲーム理論のShapley Valueになります。
このShapley Valueを機械学習に応用します。今回機械学習に応用するときにどういうことをやるかというと、モデルに投入した特徴量がM個あります。これをゲームのプレイヤーに見立ててあるインスタンスの予測値の貢献度をShapley Valueで測るというのがSHAPの考え方です。
さっきは報酬で貢献度が定義されていたんですけど、今回は報酬ではなくて予測値を使おうということですね。特徴量jが入ったときと入ってないときの予測値の差分をもって限界貢献度を計算してあげて、それをすべての順番に対して求めて平均を取るということで、その変数の重要度の貢献を計算します。
問題は、特徴量がないときの予測値をどうやって作るかということですね。アルバイトゲームの例ではA君がいるときといないときで報酬がはっきり定義されていました。これが予測モデルだと明らかではないということですね。具体的に変数が3つある状況を考えると、すべての変数があるときの予測値というのは、単純に全部の変数を入れてあげると予測値が出てきます。これでOKですよね。
それではすべての変数がないときの予測値はどうでしょう。予測値の期待値を取ってあげると、なんの情報もないときの予測値を表現できそうです。ここまではよさそうなんですが、x1だけがわかってて、x2とx3がわからない場合の予測値をどうやって作るのか、というのは難しそうですよね。これはいろいろなやり方があると思うんですけど、1つ提案されているのが、ない変数は期待値を取って消してしまう方法です。
x1だけわかっている場合だと、x2とx3に関して期待値を取って効果を消し飛ばしてしまうということですね。x2とx3の期待値を取るときの確率分布をx1で条件付けたほうがいいのか、条件付けないほうがいいのかという議論もあったんですが、条件付けないほうがよさそうだと最近の論文で言われています。
各期待値の求め方がわかったので、実際にShapley Valueを求めるときにどういうことをやっているかを見てみましょう。、例えば変数が3つあって1、2、3の順に変数を追加していくとすると、x1がわかったときに何もわからなかったときと比べて予測値がΔ1だけ大きくなります。x1がわかっているときにさらにx2もわかったらΔ2だけ予測値が変わります。
x1とx2がわかっているときに、さらにx3がわかるとΔ3だけ予測値が減ります。こんなふうに、それぞれの順番で限界貢献度が求まるので、今は1、2、3の順番で入れていますが、これを3、2、1とか2、3、1とかいろんな組み合わせで試して、平均値のShapley Valueを求めることができます。これがSHAPのやり方になります。
実際の分析例になります。PythonパッケージにSHAPというのがあります。これは簡単に使えるパッケージなので、これを使います。他にもRだとDALEXというパッケージでも使えますし、GoogleのAutoMLにもSHAPを使った解釈手法が入っています。今回はボストンハウジング(ボストンの地域別の住宅価格)のデータセットを使って、解析を行います。不動産価格を予想するデータセットです。
始めにモデルを学習させてexplainerというのをかませてあげると、Shapley Valueを求めることができます。Shapley Valueを求めたら、あとは可視化するだけですね。これはWaterfall Plotという、一番直接的なShapley Valueの使い方です。あるひとつの予測値に対して、なぜモデルがこの予測値を出したのかがわかります。(この結果を見ると)LSTATというのが予測に対して大きくプラスになっているという解釈ですね。
ここ(スライド左下)が何も情報がないときの予測値で、ここ(スライド右上)が変数が全部わかっているときの予測値で、ここ(スライド左下)からここ(スライド右上)への差分というのがそれぞれ変数一つひとつでどのくらい説明できるのかというのが表されています。
LSTATというのがかなりプラスに効いているのがわかると思います。LSTATとは貧困世帯がどのくらい周りに住んでいるかの割合なんですが、LSTATが小さい方が不動産価格が高くなるということがわかります。
SHAPはローカルな解釈手法で、一つ一つの予測値に対してそれを解釈するという手法なんですけど、適切に可視化をすることでグローバルな手法としても使うことができます。グローバルな手法としては、例えば変数重要度やPartial Dependence Plotがあります。
Partial Dependence Plotでは横軸に実際の値、縦軸にShapley Valueが取られています。これを見ると右下がりな関係になっていて、LSTATが大きくなると予測値データが小さくなることがわかったりします。
(スライドを指して)SHAPを変数重要度として使うこともできます。上にあるほど重要な変数ですね。SHAPが普通の変数重要度と比べて優れているところは、平均的な振る舞いだけではなく、外れ値もキャプチャできることです。例えばRMを見ると、基準値0の左にもすごく固まっている一方で、大きなプラスの効果が右のほう(基準値15のあたり)にプロットされています。一部の予測値では、RMによって予測値が大きく押し上げられているということですね。このように、平均的な重要度だけではなく、外れ値的なものもキャプチャできるのがいいところになります。
まとめです。SHAPを用いることで、機械学習モデルが「なんでその予測値を出したのか」を貢献度に分解して解釈できます。それはShapley Valueの考え方を応用しているので、いくつかの望ましい性質を持っています。SHAP自体はローカルな手法ですが、適切な粒度で集計することでグローバルな手法としても使うことができます。
一方で注意点があります。まず、あくまでもモデルの振る舞いを解釈しているので、モデル自体が正しくなかったらおかしなことを言うということがあります。もう1つ、あくまでモデルの一側面を解釈する一つのやり方がSHAPなだけで、モデルのすべてが解釈できているわけではないという点に注意が必要かなと思います。
以上になります。
(会場拍手)
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします