 PR
PR2026.02.26
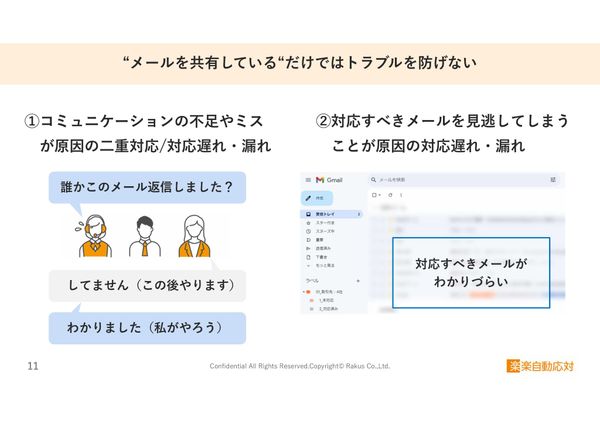
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
Semigroupとは? Monoid? 環?(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
aiya000氏(以下、aiya000):あいやと申します。今日は「Semigroupとは? Monoid? 環?」というテーマで代数についての発表をします。よろしくお願いします。
(会場拍手)
推しVimはNeovimです。活動はTwitterやGitHubなどをやっています。このスライドは「代数に興味があるけど、ちょっと敷居高いなぁ」という人に向けて作っています。
内容です。まず前半はマグマ・半群・モノイド・群というものを紹介して、後半は擬環・環・体という代数を紹介します。これらをHaskellのロジックと型で記述していきます。応用例等は重視しないですが、軽く紹介したりします。今回は用語の厳密さよりも、初心者フレンドリーな表現を心がけています。
最後に、今回いくつか型クラスや関数が登場するんですけど、形が若干標準ライブラリと違ったり、そもそも標準ライブラリに無いということもあるので、ご了承ください。あとコードの大部分はコンパイルをちゃんと通しています。ご安心ください。
本編を始めさせていただきます。まずは「代数って何?」というところから、「マグマ」という一番制約の緩い代数を説明していきます。
マグマというのは、足し算あるいはかけ算という二項演算を扱える代数構造です。
マグマはこんな型クラスで表現できます。
これが何かというのは置いておいて、インスタンスはInteger、あとリストと、BoolのAnd(&&)、Floatの+、あとUnit「()」などが、マグマの具体例としてあります。
これらの関数、「<>」や「++」と「+」って、「〜に閉じた二項演算」「〜の上の二項演算」と呼ばれるんですけど。
これは「aの値だけを取って、aの値を返す」というものです。
ここで誤解を恐れずにいうと、演算というのはHaskellだと関数のことなので、この場合下の「+」も「id」もIntegerに閉じています。
二項演算とは、2つの引数で値を返す関数のことですね。
まとめると、「+」はInteger上の二項演算です。このRationalのidは二項演算ではなくて、cons演算も閉じた演算ではないです。
マグマのまとめです。
マグマはこのようなかたちをしていて、「a」に閉じているので、何度も値を足し合わせることができるんですね。10+20+30+40みたいに。同じく、リストもマグマになります。
ここで型に対して複数のインスタンスが定まることがあります。どういう意味かというと、このIntegerの場合、プラス(+)とかける( * )がどっちもIntegerに閉じた二項演算なので、どっちにするか困っちゃいます。
Boolについても同様で、Or(||)とAnd(&&)は、両方Boolの上の二項演算になっていますね。
この解決策として、Haskellらしいというか……、newtypeを作って、newtypeを通してインスタンスを定義してあげます。
このように、マグマのインスタンスを、「足し算のa」「かけ算のa」という注釈として利用してあげます。
この上のderiving instance、どう見てもderivingですね。これStand-alone derivingという、あとGeneralizedNewtypeDerivingってGHC拡張を使っています。
Boolに対しても同じで、AndのインスタンスとOrのインスタンスをこのように分けてあげます。
もう1個あって、Xorも実はマグマとして定義できます。
なので、こんな感じで定義できます。Unitについては、インスタンスが1つだけ定まるので、ここでnewtypeは使いません。
以上で代数の導入は終わりです。次に、半群というもうちょっと扱いやすい代数を導入します。
これは、標準ライブラリに意味の上で同じもの、Data.Semigroupというモジュールで実装されています。
半群は、二項演算に加えて、左右どちらから演算しても変わらないものになっています。
この法則を結合法則と呼びます。Haskellで表すとこんな感じです
ここで便宜上Eqインスタンスを要求してるんですけど、別にEqインスタンスはSemigroupに要求されるものじゃなくて、確認するための都合というのが注意です。
では、定義はどんなものかというと、このようにマグマを継承してあげます。
関数が入ったりということはないんですけど、二項演算が結合法則を満たすというマーキングとして、このようにインスタンスを定義してあげます。
じゃあ何ができるのかというと、結合法則を満たすと、こんな感じの多相的な関数を定義してあげられます。
これは「first」という、渡された複数のMaybeの値のうち、最初の有効な値を持ってくる関数とか。あと、渡された値のうち一番大きい要素を取ってくるだとか、そういうものが定義できます。
半群ってけっこう扱いやすくて、プログラミングでもこういう関数として応用が利いて、カジュアルに使えます。
ここで、マグマだけど半群になれない例は、Double、Floatがありまして。
これ「丸め誤差」によって結合法則を満たさない、おもしろい例になっているんですね。なので、現実にある実数は半群になるんですけど、コンピュータの浮動小数点数は残念ながら半群になりません。
まとめるとSemigroupは左右どっちから演算しても結果が変わらないよという代数でした。インスタンスはこんなもの。あと、Rationalの足し算・掛け算や、Orなどがあります。
次はモノイドです。
モノイドって、みなさんもしかしたらほかの代数より名前を聞いたことあるかもしれないんですけど、これも標準ライブラリのData.Monoidに定義されています。
モノイドは、半群に加えて、単位元というものを備えた代数になります。この等式は単位元の法則です。Haskellだとこんな感じで書けます。
単位元emptyは、もう1つの値xに左からかけても右からかけても、他方を変えないという値です。
定義はこのように単純で、Semigroupに加えて、emptyって単位元を要請してあげます。そうすると、Integerの足し算については「0」、BoolのAndについては「True」がemptyになります。
例を見てみると、Integerの足し算だと3・5・7という値があるんですけど、ここに0をどっちから足し合わせても変わりませんよね、ということになっています。
このようにモノイドは、emptyを適用することで自明な初期値を自動で適用できます。
どういうことかというと、例えばsum関数を考えてみると、sum関数は初期値は0ですよね。その上からほかの与えられた要素の数を足していって総和を求めるという、そういう性質なんですけれども、まさにモノイドですね。
allも同じで、初期値がTrueです。
まとめると、モノイドは自明な初期値が定まった代数です。
ほかのインスタンス。
Integerの掛け算とRationalのかけ算。あとリストです。これはemptyの1と、あと空リストが単位元になります。
あとは、OrとXorもあります。Rationalの足し算もあります。
UnitはUnitです。
インスタンスになれない型として、NonEmpty Listがありまして、空リストがないので単位元がないんですね。
あとは、FirstとLast。これはMaybeのnewtypeなんですけど、最初の有効値を探して持ってくるのがFirstで、そもそも渡されたものが何もないと一番最初というのは考えられないので、モノイドではないです。
こんな感じで、emptyは、左右から足しても他方を変えない値になります。
では次の代数。
群という、けっこう制約が強い代数がありまして、群ではあるaの値xに対して、xの逆元というものが1つ定まります。
これをHaskellで書くと、このようにinverseという関数として表現できます。
「xとxの逆元を足し合わせると単位元になる」という法則ですね。
Groupは、モノイドを継承して、ある値に対してその逆元を取ってくる関数を追加したものになります。例えば、Integerの足し算だと、「10」とかそういう値に対して「-10」みたいなマイナスの値を取ってくるものです。Xorは実はidentity関数で、xの逆元がxそのものというかたちになります。
Integerの足し算は、こんな感じで0になりますね。
Xorについても、TrueとTrueはFalseになるし、FalseとFalseはTrueになります。ということで、法則を満たします。
モノイドであって群でない例はけっこうあって、これらは群になれないです。
AndだとFalseの逆元がなくて、OrだとTrueの逆元がない。考えてみるとわかるんですけど、片方がFalseだとAnd演算ってTrueにならないですよね。Or演算も同じで、片方がTrueだとどうしてもFalseにならないので、群にはなれないことになります。
リストも逆というものがないんですね。まさに群じゃない代表的な型だと思います。
Product IntegerとProduct Rationalはなりそうで、10の逆元は「1/10」って気がしちゃうんですけど、「1/10」はIntegerじゃなくてRationalなので、残念ながら逆元がないです。Product Rationalも、「0/x」に対して「x/0」というゼロ除算を発生させてしまうので、残念ながら群にはならないです。
群の応用は数学分野に強いかなと思います。個人的にはプログラミングで直に触れるのはあんまりないんじゃないかなと思います。
ほかのインスタンスはこんな感じです。Unitはいつものやつです。
まとめると、群aは、aのすべての値に対して、それの逆元が定まるものです。インスタンスは、IntegerとRationalの足し算、BoolのXorと、Unitがあります。
というところで、ちょっと寄り道をしてみます。半群とモノイドと、全部のところで横断する概念で、「可換」というものがあります。
「可換である代数とはなんぞや?」というと、xとyを足し合わせるのとyとxを足し合わせるのが同じという性質です。
この法則を交換法則といって、また可換とか言ったりします。
可換な半群は「可換半群」「アーベル半群」と言ったり、モノイドと群についても同様、「可換」とか「アーベル」とかって言います。
Haskellで書くと、交換法則はこのように書けます。
Abelianというのが可換半群、あとは可換なほかの代数のマーキングとして、インスタンスを定義します。
これの応用例として、ユニフィケーションという分野があるんですけど、それはなんぞやというのはここではあまり説明しなくて。端的にいうと、この1とCharのリストをConsするのは正しいのかそれとも正しくないのかという型推論に使えます。
半群であって可換半群でない例というとリストですね。リストは後ろから足し合わせるのと前から足し合わせるのじゃ順序が変わっちゃうので、違います。
というところで、Abelianはこのように定義できて、インスタンスはこのように定義できました。リストなどは交換法則を満たしませんでした。
ここで前半戦は終わりです。ここまでのまとめは、マグマ・半群・モノイド・群は、それぞれこのような要素を持っていました。
このように、「より強い代数」=「より弱い代数+何か」というかたちで定義されます。
というところで、後半編です。
まず、擬環という「Rng」という代数があります。これは、可換群と可換半群の両方の性質を持った代数です。
分配ができる。分配というと、小学校の頃習ったかもしれないんですけど、下の等式を満たすような性質のことです。
Haskellで表すとこんな感じ。
ここで今まで使っていた二項演算を「加法」と言って、先っぽが内側に向いている演算子、加法と向きが逆になったものを「乗法」って呼びます。
Rngの定義はこんな感じでできるんですけど、そのうち加法群は、加法の二項演算って、emptyAとinverseAが加法群の部品になっていて、乗法半群は乗法二項演算になります。
加法群は群なので、このように加法の単位元、零元って呼んだりもするんですけど、あと各値に対する逆元が定まります。
擬環は、要するに「分配をできるよう定まったプロトコル」という捉え方ができます。
インスタンスとしては、まずInteger、この分配がみなさんに親しいんじゃないかなと思います。ここで足し算とかけ算、区別がなくなって、両方持っているのでnewtypeが消えました。
RationalもIntegerと同じ定義。
BoolはXorとAndの合わせになっています。
あとUnit。これはいつものですね。
というところで、擬環は一番シンプルに分配ができる構造でした。
こんな感じでインスタンスがあります。
次に、1つだけ擬環に概念を加えた「環」という代数があるので、軽く紹介します。
加法の可換と、あと乗法のほうがモノイドになっています。
乗法のほうに単位元がかかってくるので、RngにemptyM、multiplicative(乗法)のMを足してあげます。
これはかけ算についてなので、かけ算の単位元は1ですね。
Boolは、Andの単位元なので、Trueを定義してあげます。
Unitについてはいつものってことで。
こんな感じの、擬環をちょっとだけ拡張してあげたものになります。
必要な概念なんですけど、今までの流れとは違うものを紹介します。話半分で聞いてもらっても大丈夫です。
みなさん、写像は好きですか? 簡単に写像って何かというと、こんな要素から要素へ割り当てるものですね。
ここで写像をちょっと拡張したものとして、半群の準同型写像というものを考えます。
半群の準同型写像というのは、まず半群が2つa,bとあって、この二項演算を「!」と「?」で区別します。
そのときに、aの値x,yがあったときに、このような等式を満たすようなfです。
「なんのこっちゃ?」てことなんですけど、準同型写像を表すHomoという型を定義してあげます。
これはaからbへの関数のnewtypeです。そして、ListからIntへの準同型としてlengthを定義できます。それを「ListAToInt」という名前で定義してあります。
このListAToIntは、先ほど書いたこのような法則を満たします。
ところで、これは半群に対するものだったんですけど、さらにモノイドに対する準同型写像や。
群に対するものがあります。
実は自己準同型写像とその合成はまたモノイドになるんですね。
ということはこの「Homo a a」みたいに行き先と行く元が同じ準同型写像は。
こんなふうにモノイドインスタンスが定義できます。
あとは、このreverse、duplicateという準同型写像があったときに、このような感じに、また別の準同型写像を合成として定義できます。
イメージはこんな感じ。
reverseはリストからリストへの準同型なんですけど、さらにそのreverseは自己準同型写像のものの値になります。
みなさん、すべての道はモノイドに通じます。どうぞ、この言葉をお土産に持っていってください。
(会場笑)
最後に、「体」という代数を説明します。
これ、全部のっけみたいな代数なんですけど、加法と乗法が両方、群です。ただし、乗法のほうは0を除いたものです。0を除くというのは、あとで見ていきます。
これ実は四則演算ができる代数なんですね。
「なんぞや?」というと、環に対して乗法逆元をまず加えてみます。インスタンスは、基本的なデータ型だとRationalぐらいしかなれないような厳しい制約を体は持つので、Rationalだけ。
0 ≠ 1というような、加法単位元と乗法単位元が異なることを要請するものですね。ここでいつものUnitさんはお亡くなりになってしまいました。Unitさん、またね。
(会場笑)
乗法逆元は、群でやったところと同じなんですけど、各値に対して逆元が定まります。
ただし、0を除くというのをRationalで見てみると、このようなR’という型に対して乗法群が考えられます。これは0、1/0、0がないんですね。というものに対して乗法群を考えて、あと普通に加法群を考えると、体が定義できます。
「0を除く」ってやらないと、実は、「0 = 1」とか「0 = a」だとか、全部0になるんですよ。びっくりですね。
(会場笑)
体は四則演算ができるものでした。
四則演算ができるっていっても、「引き算、割り算はどこ?」って思うんですけど、このように定義できます。
例えば、引き算は、足すの後ろ側にマイナスをつけてあげると、ちゃんと引き算になります。同じように、かけ算に対して後ろの分母と分子を入れ替えてあげると、ちゃんと割り算になってくれます。
最後のまとめです。
体は、環に加えて、乗法の逆元を求められる構造です。インスタンスは基本的なデータ型のうちRationalぐらいしかなかったです。
今日の内容はここまでです。おつかれさまでした。最後にまとめ。
代数はこのような7つ、あとそれ以上とか、各々のレベルで構造に制約を課してくれるものでした。どんな制約かというと、こんな感じでした。
最後に宣伝。こんな本を出しています。もし興味あったらよろしくお願いします。
以上で発表を終わります。ご清聴ありがとうございました。
(会場拍手)
司会者:質問のある方はいらっしゃいますか?
質問者1:すいません。全部の発表に質問してしまって申しわけないんですけど、ちょっとわからないところがあって。可換というのはユニフィケーションに使えるという話がちょっとわからなかったので、もう少し詳しく教えていただけますか?
aiya000:はい。ユニフィケーションってあるものが別のものと同じかどうかを調べることで、例えばこの式だと、1というNum aの値があって、もう他方はCharのリストがあります。Consは要素とリストをとるので、ここでNum aと Charが同じかどうかというところを調べられます。
ええと……どうしよう。 Wikipediaさんに聞くとぜんぶ答えてくれちゃうんですけど。
(会場笑)
やばい。あんまり理解していないことがバレてしまった……。
(会場笑)
質問者1:時間がかかりそうであれば、懇親会とかでも大丈夫です。
aiya000:ごめんなさい。お願いします。
質問者1:はい。ありがとうございました。
司会者:ほかに質問のある方はいらっしゃいますか? ちょっと数学数学した内容でしたが。はい、ありがとうございます。
質問者2:質問というか、ちょっと補足なんですけど。普通は代数的構造を代数とは言わないと思います。
代数的構造というのは、群とかモノイドのように、要素、つまり集合とその相手の演算が与えられる構造であって。一方、代数というのはもっと特殊な場合を指すことが多いですね。
私もあまり代数に詳しくないんですけど、有名なものだと何があるでしょうかね……。そうですね、環上の代数とかが有名ですかね。あと、リー代数とか。だから、できればそこは用語は正しく使っていただければなと思いました。ありがとうございました。
司会者:それでは休憩時間に差し支えているので、このへんにさせていただきたいと思います。あいやさん、ありがとうございました。
(会場拍手)
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします