 PR
PR2026.01.19
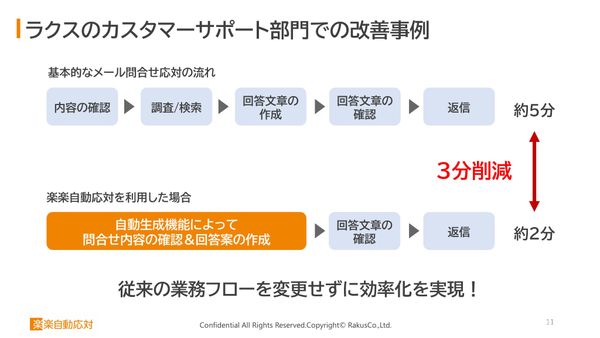
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
コピーリンクをコピー
ブックマーク記事をブックマーク
野村将寛 氏(以下、野村):簡単に自己紹介をさせていただきます。僕は今、サイバーエージェントのAI Labという研究組織に所属していまして、ハイパーパラメータ最適化の研究をしています。先ほどの午前中のセッションで、AutoMLのセッションがあったと思うんですけど、そちらで発表していた芝田のチームメンバーになります。
産総研でもハイパーパラメータ系の研究をしていまして、東工大小野研究室というところの社会人博士の学生でもあります。進化計算というブラックボックス最適化の分野があるんですけど、こちらの研究をしています。
では、始めにハイパーパラメータ最適化の説明をさせていただきます。まず、機械学習手法にはチューニングすべきハイパーパラメータというのが存在します。
例えばロジスティック回帰であれば学習率・正則化係数、SVMであればカーネルの種類・またはカーネルの種類に紐付くパラメータ・正則化係数、Deep Neural Networkであればユニット数・レイヤ数・学習率・ドロップアウト率だったり、さまざまあります。こういったハイパーパラメータを最適化する問題が、ハイパーパラメータ最適化問題になります。
じゃあこのハイパーパラメータ最適化問題について、失敗するとどうなるかというのを多項式回帰の例を参考に見てみます。少し見づらいんですけど今やりたいことというのが、右側の青い点線が真の関数で、そこからサンプルが青い丸が得られているとします。これに対して多項式をフィッティングするという問題です。
今、このminimizeの右側の式の第2項目のところでψに紐付いているλというのを、うまくチューニングして正則化したいという問題です。もし、これをうまくチューニングできると右側の図の緑色の線みたいにうまくフィッティングすることができるんですけど、例えばλを0にして、まったく正則化しなかった場合については、かなりサンプルに対してオーバーヒットして真の関数の予測に失敗します。
一方で、このλというのを大きくし過ぎると、右の図の赤い線のようにモデルを単純化し過ぎしまって、うまくフィッティングができていないということになります。なので、この右側の緑色の線みたいにうまくチューニングをする必要があります。
このハイパーパラメータ最適化の流れを一度おさらいしてみたいと思います。今はロジスティック回帰の例を参考にします。このロジスティック回帰では学習率ηと正則化係数Cを設定する必要があります。
ということで、まずはηとCを……例えばη=0.1、C=100と設定しますと。設定したら、このハイパーパラメータを使ってtrainデータに対して学習パラメータを最適化します。
この最適化した学習パラメータを使って、Validationデータに対してValidationエラーを求めます。例えば、0.8というValidationエラーが得られましたと。
ということで、ここではValidationエラーを小さくするようにハイパーパラメータを決めるという問題です。このηの値とかCの値を変更して、再びtrainデータに対して学習してValidationデータに対して予測をするという問題ですね。
今注目していただきたいのが、このロジスティック回帰については、とくに何も考えずに何かハイパーパラメータを設定したら何か値が出てくるととらえることができます。
なので、この問題を抽象化すると、ブラックボックスな関数の最適化と捉えることができます。ここで言うxというのが先ほどのハイパーパラメータで、ここで言うf(x)というのが先ほどのValidationエラーとかですね。
ということで、ここの段階でハイパーパラメータ最適化問題というのはブラックボックス最適化問題として捉えることができるとわかったので、次からはブラックボックス最適化の説明をさせていただきます。
ブラックボックス最適化とは、先ほど言ったように関数の中身がブラックボックスなので、勾配情報などは使えません。なので、一般的な最適化であれば勾配法とかで勾配を使って計算ができるんですけど、それができない問題になります。この問題の重要な仮定としては、1回の評価に時間がかかることを想定しています。
例えば、Deep Neural Networkのチューニングであれば、ハイパーパラメータを1個決めて1個の評価値を得るためだけに1時間ぐらいかかることがあります。ということで、この問題ではいかに少ない評価回数で最適化を行うかというのが大事なポイントになります。この発表ではブラックボックス最適化において有力なCMA-ESとベイズ最適化についてお話します。
まずはベイズ最適化です。ベイズ最適化はハイパーパラメータ最適化問題において一番人気のある手法で、ご存知の方も多いかなと思います。このベイズ最適化において本発表では最もベーシックかつオープンソースとして簡単に利用できるGP-EIという手法とTPEという手法について解説します。
まずはGP-EIについて解説します。GP-EIを一言で言うと、ガウス過程GPによって目的関数をモデル化します。このモデル化した結果を使って評価値の改善量の期待値が最大となるようなxを選択するということを繰り返して最適化する方法です。こちらについて図を用いて説明します。
今、この青の線が真の関数です。こちらについて最適化を行っていきます。
最小化問題を仮定します。まずはGPによって赤のサンプルが今得られているサンプルだとして、このサンプルを使ってGPによって目的関数に対してフィッティングさせます。見づらいんですけど、薄いピンクのところが95%信頼区間になっていて、ピンクの点線がGPが予測している平均になります。
ここで大事なこととしては、今得られているサンプルの近くというのは確信度が高いので分散が小さくなっているんですけど、今得られているサンプルから遠いところに関しては分散が大きくなっているということです。このGPは目的関数がわかっているところはちゃんと分散を小さくして予測してくれるし、わからないところは不確かさを考慮して分散を大きく見積もってくれるというところです。
続いて、この上の式でどの辺りの領域が良さそうだったり、まだ探してないからいいかもしれないというのがわかったので、これを使ってEIという先ほどの評価値の改善量を計算します。今のこの下の図のグリーンの線がEIの値になっています。このEIの値を一番大きくするxというのが評価値を良くしそうなxになります。今このグリーンの中で一番大きなところを探すと右端になっているので、右端の点を評価します。
そして次のイテレーションに入って……ちょっと右端で切れちゃっているんですけど、ここで右端の点を評価してGPを更新し直します。そして再度EIを計算をして最適化をすると一番大きな点が真ん中になっているので、この点を評価します。これをどんどん繰り返すことによって最適化を行っていくというのがベイズ最適化のアルゴリズムになります。
ちょっと詳しい式について説明するんですけど、EIの式というのはあるxに対してそのxを評価したときに今の最良評価値からどれくらい改善ができるかという式になります。今のこのy⁻というのが最良評価値なんですけど、今は最小化を仮定しているので、もしこのy⁻よりも小さい評価値が得られたらここの部分がプラスになる感じですね。
こちらがp(y|x)のところで、これはxに対してyがどのあたりに分布しているかというのをガウス過程によってモデル化する部分になります。今のこのEIというのは目的関数がGPに従うという仮定をおいた場合には、このp(y|x)のところが正規分布に従うという仮定ができるので、この場合はxに対するEIというのは解析的に計算ができます。
なので、これでxを一番大きくするxを探せばいいじゃんとなるんですけど、この問題は多峰性関数になってます。例えばこれとかなんですけど、下の図を見ていただくとわかるように大きな山というのが何個かあったりします。これは一次元だとけっこう簡単に見えるんですけど、高次元になるとかなり難しい最適化問題になります。
ここに関してはオープンソースによって実装がけっこう変わっていたりします。例えば論文であるのが離散変数とかに関してはEDAという進化計算手法を使って最適化して、連続変数に関してはCMA-ESを使ったりとか、論文によってけっこうさまざまな最適化が行われてたりします。なのでオープンソースとかで自分で実装するときにはちょっと注意が必要かなと思います。
続いて、TPEという手法について説明します。このTPEというのをあまり聞きなれない方も多いと思うんですけど、HyperoptやOptunaがデフォルトで採用している性能の良いアルゴリズムになります。このTPEはEIを使うという点まではGP-EIと同じなんですけど、モデル化の部分がGP-EIと違います。具体的にはGP-EIがp(y|x)をGP-EIで直接モデル化をしていたんですけど、その代わりにp(x|y)とp(y)でモデル化をしています。
具体的なモデル化の式なんですけど、ある閾値yというのを用いて、評価値上位と下位からなるp(x|y)というのを以下の式で定義しています。ここで上のl(x)というのがある閾値よりも低い、つまり評価値が良いほうですね。g(x)というのが評価値が悪いほうです。じゃあこのyをどう決めるかというと、これは分位点を使って決めます。この一番下の式ですね。
例えば、このγが0.1だったら評価値上位10パーセントの解の確率密度関数をl(x)で推定して、下位90パーセントをg(x)で推測するというかたちになります。これらのモデル化を用いると先ほどのEIの式というのは、がんばって計算するとこの右の式のようになります。このEIを最大にするxを探すと評価値の改善の期待値が最大にできるので、xに依存する部分を探すとl(x)/g(x)を最大とするxがEIを一番大きくするということがわかります。
このl(x)/g(x)というのは評価値下位に属する確率を小さくして評価値上位に属する確率を大きくするという直感的な式になります。こちらのEIの値を大きくするという意味合いなんですけど、今は評価値上位の確率密度関数がl(x)で右側の赤い関数ですね。評価値下位の確率密度関数がg(x)で右側の青い関数です。そうすると、この確率密度関数の密度比になっています。
なので、できるだけ評価値上位に属する確率を大きくしたいんだけど、一方で評価値下位に属する確率を低くしたいというところにEIが選ばれるようになります。
じゃあこのGP-EIとTPEでどっちがいいんだという話になるんですけど、いくつか選ぶ基準があるかなと思っています。
まず1個はカテゴリカル変数の取り扱いです。このTPEという手法に関しては評価値上位と下位について確率密度関数を構築できれば使えるんですけど、GP-EIに関してはガウス過程を利用するためには直接使えないので工夫が必要です。
具体的にはone-hotエンコーディングをして連続変数とみなしてしまう方法だったり、カテゴリカル変数用のカーネルを設計してGP-EIに食わせられるようにするといったことが必要になります。一般的なオープンソースではone-hotエンコーディングを採用している例が多いかなと思います。
続いて次元数になります。こちらはEggenspergerさんが論文で調査しているんですけど、ロジスティック回帰、SVM、LDAなどのチューニングタスクをたくさん解いたときに、結果としては次元数が低い、つまりハイパーパラメータの個数が少ない問題に関してはGP-EIのほうが良い性能だったと。一方で次元が高い問題に関してはTPEのほうが良い性能だったということを報告しています。
これの僕なりの解釈を述べます。まずは、GP-EIに関しては探索空間全体に関するモデル化が必要になります。基本的に、次元数が増えると体積空間は指数的に増大するのでスケールしづらいという問題があります。一方で、TPEというのはすでに存在する点から評価値上位の確率密度関数を見積もって、評価値下位の確率密度関数を見積もるということをするので、直感的には探索空間全部を探すというよりは、いい感じの部分空間を選んだらその付近を探すという挙動をします。
ということで、GP-EIだとそもそも空間を探し過ぎてぜんぜん良い点が選べないということが起こるんですけども、そういった挙動はTPEだとあまりないというのが要因として1つ挙げられるかなと思います。
続いて、CMA-ESの説明に入ります。CMA-ESとは進化計算手法における有名な手法の1つです。近年だと、ハイパーパラメータ最適化にもけっこう使われている手法です。このCMA-ESの動きをすごく簡単に説明すると、多変量正規分布から解を生成します。この多変量正規分布をいい感じのところに動かすことによって、良好なサンプルを得るというものになります。
こちらも動きを簡単に説明します。まず最適解が左下にあって、等高線がこのようにあるとします。
今、正規分布が右上にあるとします。CMA-ESでは、まずここから正規分布をサンプルします。このサンプルしたそれぞれの解に対して評価をします。良い解だったら大きな重みに、悪い解だったら小さい重みにと重み付けを行います。そして、この重み付けを行ったものを用いて、正規分布のパラメータを更新します。
つまり、正規分布のパラメータなので平均ベクトルと共分散行列のどちらも更新します。これだけ見るとすごく直感的なことをやっているんですけど、これを統計的に解釈した論文が数年前に出ていて、これは何をやっているかと言うと、正規分布からサンプルされる解の期待評価値を小さくする方向、つまりこの正規分布からサンプルされる解が評価値がだんだん下がっていく方向に(確率分布のパラメータを更新するという)自然勾配法的な解釈ができるということです。
なので、統計的には確率分布の空間で勾配法をやっているという解釈ができます。
では、GP-EIとCMA-ESの比較を行います。Frank Hutterさんという方が、論文でさまざまなベンチマーク関数を用いてGP-EIとCMA-ESの比較を行っています。結果としては、今僕らが評価できる回数が少ない場合、具体的には10×次元数ぐらいの場合に関してはGP-EIのほうが性能が良いですと。一方で、評価できる回数が100×次元数ぐらいの多い場合に関しては、GP-EIよりもCMA-ESのほうが良いという報告がされています。
こちらについても解釈を述べます。まずGP-EIに関しては、先ほども言ったように探索空間全体に対してモデル化をします。ということで、評価回数が増えたとしても、ある1個の点をどんどん改善し続けるという挙動があまりないので、収束性はあまりよくないです。その一方でCMA-ESは、現在の正規分布さえ更新すればいいということで、直感的には勾配法にけっこう近くて、今の正規分布内しか見ないということですね。なので、収束性は良いです。
続いて時間計算量の面から見てみます。GP-EIの計算量はイテレーション数tに対して3乗になります。それに対してTPEは線形オーダーで、CMA-ESは依存しないです。まずGP-EIの3乗の理由については、これはある点に対する(事後分布の)推論、プレディクトがカーネル行列のインバースが必要になるので、3乗かかりますと。TPEに関しては、そういった操作とかは必要ない(カーネル密度推定のみで良い)ので線形オーダーで済みます。
そしてCMA-ESについては、そもそも過去のサンプルを全部使ったりすることがなくて、今の正規分布をどんどん動かしていけばいいだけなのでイテレーション数には依存しないです。それもあって先ほどの結果を踏まえると、基本的に評価回数が膨大にある場合というのはベイズ最適化よりもCMA-ESのほうがいいんじゃないかなという結論が得られるかなと思います。
こちらが、僕の主観込みのブラックボックス最適化チートシートになるんですけど、高次元・カテゴリカル変数・バジェットが高いか低いかによってざっくりとした手法の相性がこちらになります。ポイントとしてはTPE、今のHyperoptとかOptunaが採用しているアルゴリズムですね。TPEに関してはそんなに失敗する問題ケースというのがないので、安心して使える手法かなと思います。
一方で、バジェットが大きい場合については、CMA-ESの挙動というのはベイズ最適化に比べるとけっこう理想的な挙動になっているので、こちらを使うという選択肢が有力かなと思います。
次に、注意が1点あるんですけど、最適化の分野でノーフリーランチ定理というものが知られています。これの定理の意味なんですけど、すべての関数に対する最適化手法の平均的な性能というのはランダムサーチに等しいということが言われています。もうこれは証明されています。つまり、僕らは問題クラスを仮定しないと、強い最適化手法というのはそもそも作れないという定理ですね。
今はベイズ最適化とかがハイパーパラメータ最適化問題に対して有力というのは、ハイパーパラメータ最適化問題の問題構造というのにベイズ最適化がヒットしているということになるんですけど、ここでハイパーパラメータ最適化問題の難しい点として、ハイパーパラメータ最適化問題は僕らが探索空間を定義できるんですよね。
例えばDeep Neural Networkのチューニングをする場合に、学習率0.001から0.1までチューニングするのを、仮に0.001から0.5にしてもいいし、その0.001から0.01までチューニングするのを線形変換で作ってもいいし、対数のスケールに落として変換してもいいしという、僕らが空間に対する自由度を握っています。
ということで、けっこうユーザが設計する探索空間に依存しますということで、この手法が良いと言うことは一概には難しいんですけど、このガイドラインは参考程度に見てもらえるといいかなと思います。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします