 PR
PR2026.02.26
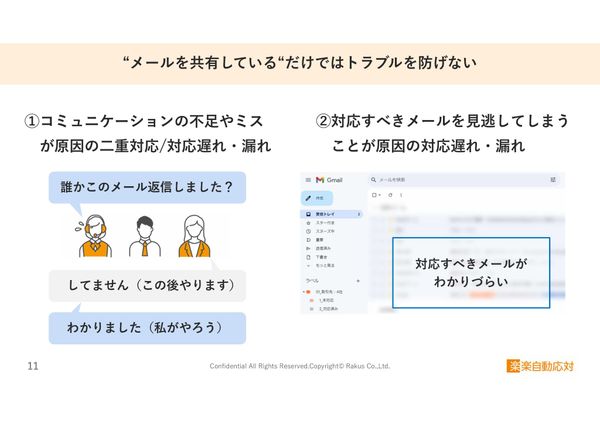
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
数理モデル化と問題解決(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク

松田健氏(以下、松田):(入場テーマ曲が)予想以上に恥ずかしい感じで来ましたけれども(笑)。静岡理工科大学の松田と申します。「数理モデル化と問題解決」というところの話ですけれども、この分野かなり話題性が広いので、どちらかというと半分ぐらいは私の話です。
もうちょっと細かく言うとこれには数学の話が結構出てきまして、それだけ聞いていると頭が沸騰してしまうと思うので、皆様にも考えられるような問題を出しながら、話を進めていきたいと思います。

タイトルをどうしようかと思いましたが、勝手に「特徴の着色」とつけて話を進めていきたいと思います。今から私が話をするのは着色という話ですが、これと数理モデルや数学の話を、どういうふうに関係付けていくか? という点についてはそんなにうまくまとまっていないので、皆さんでくみ取って聞いてもらえるとありがたいです。
着色というものについて話をすると、例えば生命科学の分野だったら、タンパク質に色をつけたら病気のことがいろいろわかるのかもしれないですね。ちょっと私は生命科学には詳しくないのですが、例えば細胞に色をつけて細胞分裂を観察できると、教材として使えるのだと思います。
情報の分野ではどんなのがあるかというと、エクセルに色をつけるのもありますね。他にもヒントン図と言われているものもあって、パターン認識と機械学習(PRML)でも紹介されています。
行列の各要素が正方形で表されていて、白が正、黒が負、面積が要素の大きさを表しています。こういうのも1つの可視化だと思うんですよね。可視化のやり方もいろいろとあると思いますので、そういうふうなところを話していきたいと思います。

私は一応、応用も結構やっているんですけれども、Webアプリをねらう攻撃の自動検知とかですね。大体どういうことをやるかというと、入力があるわけですね。プログラムコードの一部を入力するものと思ってもらえばいいと思います。
その中に悪意のあるものがあれば、攻撃に繋がる。「悪意のあるコードを含まない」とここでは微妙な書き方をしていますけれども、なかなか機械だけで悪意があるかどうかを判断するのは難しいわけですね。文字列が入力で、出力としては攻撃か正常か判断する。これが検出のモデルの1番簡単な部分だと思います。

ここも非常にいろんなやり方があるんですけれども、入力ってWebアプリをねらう攻撃だとすると、基本的に文字列ですね。プログラム言語です。ここから出力yが攻撃かどうかを当てたいわけですね。
これを計算機的に処理するならば、文字列を何らかの数値データにする必要があり、ここが結構大事だったりします。
攻撃検知を実現するには教師あり学習を考えるのが良いと思いますが、教師なし学習を上手に使う方法を考えても良いですね。
とにかくモデルf(l.θ)のlの部分が文字列に対応する部分ですから、文字列lを何らかの数値xに変えてf(x.θ)とします。その後はパラメータのθの部分を推定する方法を考え,そこから何らかの判断基準を作ることによって、初めて予測というのが成り立ちます。
問題は未知データにどうやって対応するか? とか、予測を間違えることがあるのでそれをどうするか? とかですね。モデルについても考え方が色々で、さらにパラメータの学習方法も色々あるわけです。このような中で良い予測をするためにどうするかということを考えていかないといけないわけです。

学会に行けば関連する話を色々聞けると思うので、細かい話はここではしませんが、目標としてはやっぱり100パーセントにしたいですよね。これは正直、たぶんほとんど無理でしょう。なかなか100パーセントにはいかない。
これをうまくやればあるデータセットに限っては、それは100パーセントにいけるでしょう。でも未知のデータというのは、全部を集められるわけがないのでね。たとえ正解率が高くてもですね、攻撃検出っていう観点でいくと、なぜ間違えたのか? というのを説明できないとちょっとpoorな感じですよね。
その間違える原因というのは予測をするためのルールで検知するので、「これはこういうルールで検知しているんだな」とわかってしまったら、その穴をついた攻撃というのはいくらでも出来るわけですし、まったく新種の攻撃がきているかもしれない。ここまで機械に判断させることがちょっと難しいということは、なんとなくわかるかなと思います。

少し攻撃検知から離れてみると、これはロシアの例ですかね? 風呂に入って防水のスマホを扱っていて、多分バッテリーを電源から充電していて、それを風呂に落として感電死したという話ですね。
例えばこういうふうに、(防水の)スマホを風呂に持っていくということは普通に考えられるわけですよね。しかし、このような状況で、風呂の間に「充電しながらスマホ」というのを予測するというのは、そんなに簡単なのか、難しいのかよくわかりませんよね。これも1つ予測だと思うんですね。
こういうふうな事が出来るんだという上で、どんな危険性があるかということを予測するという。これは、こういう事故が起こったからわかるわけですけれども、「事故が起こる前からこういうことが予測できるのかな?」っていうのは、なかなか難しい話ですよね。

誤検出の問題で、これは数理統計学ではフォールスポジティブとかフォールスネガティブと呼ばれているものですね。第1種過誤とか、第2種過誤というふうに教科書には書いてあると思います。
第1種過誤というのは冤罪ですよね。悪いことをしていないのに、悪いことをしたという決めつけです。第2種過誤は、悪いのに悪くないと判断することです。これらはどっちが悪いかというのは、その分野によって違うわけですけれども、このような誤判別が起きる原因というのは何だ? ということを考えていくのも、大事な話だと思います。
この図は特徴がどうなっているのかというのを調べて、何とか予測できるかな? ということを考えているわけです。ただ判断基準みたいなものを決めてデータを分離するだけでは、なぜ誤判別が起きたかということはわからないわけです。

この辺で着色の話が出てくるわけです。自動検出とかをやる最初の目標は何かというと、当然人間の支援を目的としているわけですよね。なので攻撃検出自動化の目的が支援であるならば、検出してあげるのも支援です。
しかし例えば、これは時代の流れと逆行するかもしれませんけど、攻撃されているかどうか一目でわかるような工夫を入れてあげるというのも1つの支援ですね。これはですね、目Grepという言葉を皆さん知っているかどうかわからないですけれども、バイナリデータに色を付けて、そのファイルの構造を当てるというやつです。あとでちょっと例を出してみます。
この部分でみなさんにちょっと、簡単な問題を出したいと思います。一目でわかる工夫を着色でやってあげることでいうと、アクセシビリティとかもあると思いますが、これをすると、ここはまだ期待ですけれども、例えば攻撃データに色がつく。そうすると攻撃じゃないものにも当然色がつくわけですよね?
それに見慣れていくと、そういう技術力がある人にも、さっきのように第1種の過誤とか、第2種の過誤っぽいのが、可視化されていくのかもしれないという期待を持てるかなと思います。できるかどうかわかりませんが。

それでですね、これは目Grepなんですけれど、皆さんが知ってるやつとはきっと違う問題です。これはあるファイルのバイナリですね。バイナリと言っても16進数で表記されています。
左側は色を付けて可視化しているわけですね。この256個の値の何番から何番までが何色なのか? みたいな感じでやっているわけです。1番先頭にいくと、このファイルが何かということがわかるんです。
このファイルはなんでしょう? これは多分誰も当てられないと思います。

皆さんはこれ知ってます? 去年山形新幹線、「とれいゆ」という足湯がついている新幹線に乗ってきたんですけれど、この写真はビットマップで、これをバイナリエディタでわざわざデータをバイナリにして、違う色を付けて、それをばらばらに見たものです。
バイナリエディタの色づけされている部分をみると画像のこの部分かな? ということがある程度推測できるかと思います。

次の問題は全然大した問題ではないですけれども。これ何の写真だと思います? 別にこんなの当てたって大したことじゃないんですよ。本当の目Grepの問題とはまた違う問題ですからね(笑)。だけどこれは画像がビットマップだからこういう特徴が出て、こういうくだらない遊びが出来るわけです。
ヒントはですね、静岡県です。私静岡理工科大学ですから。あ! 富士山という声が聞こえた気がするけど……正解です。富士山ですね(笑)。
これビットマップだったら絶対こういう遊びが出来るかというと、実はそうでもないんですけれども、問題があと2つあります。

さあこれは、たぶん1番上かな? ここにビットマップって書いてるんですね。これなんだと思います? さっきの富士山のやつも見ていて、湖面に映っていたものが逆に映っていた部分が、ああいうふうに出ていたわけですね。これはなんだと思います? これは静岡とはちょっと関係ないかな。
ヒントはですね、鎌倉のほうですね。はい、正解にいきます。
大仏さんです。この辺が色づけの部分に出てたかなと思います。こうしたように、確かにビットマップはこんな特徴を持ってるんですけれども、どんな画像でもうまくできるかといえば、そうでもない。あと、何ビットずつに色を付けるかというところでも、変わってくるんですね。

もう1つ。これは高校生向きの話をする時に使ったネタなんで、しょうもないネタなんですけど、これなんだと思います? これはですね、キャラクターです。皆さんが良く知っているキャラクターじゃないですか? 色を見たらわかりますよ。
最後は誰かに答えてもらいたいところですけど、答えられる人はいますか? はい。
会場:ふなっしーです。
松田:正解です。素晴らしい。別にこんなの当たっても何も嬉しくないと思いますけれども、ふなっしーです。

自分の研究の話ばっかりになってしまっていますので、運営委員をやっていますMPS(数理モデル化と問題解決研究会)の話をします。まずは私の学生たちが発表する内容について少しだけ紹介させてください。
着色に関して攻撃検出のところでやっているのが1つと、他のファイル情報の特徴抽出に関するの発表会があります。この下の2件はこれから話をしていくところとちょっと関係があって、ここから数学の話になります。
多分ですけど、これから言う話は、もしかしたら皆さんは聞いたことがないかもしれない。ちょっと難しいかもしれないですけれども、知っておくと有益なることもあるかもしれないという期待をこめて。

もうちょっとしたら数式が出てきます。攻撃データの着色の研究は、攻撃データの重要な部分に色をつけることで、「正常なデータと比較すると何か違うな」ということ分かり易くできないかということを目的としてやっています。
着色したものを素人の人に見てもらって、「確かに違うよね」っていう声が聞けるかどうか私の興味があるところではあります。

数理モデル化と問題解決の部分の一般的な話をしろと言われるとすごく難しいので、これはMPSの研究会の101回だから多分前回かな? なるべく去年の4月以降のやつで発表タイトルの頻度解析をしてみました。キーワードをみてどんな発表があるか調べているだけで、それ以上やそれ以下の目的はありません(笑)。
これはタイトルの頻度回数ですね。距離だとか、画像だとか、株とか、環境とか、変化とか予測とか、それっぽい、最近の流行りっぽいやつが入っているなと思います。

ちなみにMPSとNIPS(Neural Information Processing Systems)を比べるのはどうかと思いますけど、NIPSといえば機械学習系だとすごく大きい国際会議です。
こちら側を見てみますと、英語ばっかりです。それが国際会議なんですけれども。どうですか?
ちょっと気がかりなのは、これMeCabでやったんですけど、Monte Carloはたぶんワンセットだと思うんですけれども、なぜかMonteが6で、Carloが4、他のCalroはどこに行ったんだろう? これちょっとわからないんですけど(笑)。
ClassificationとかDecisionだとか、Decompositionとか、Densityとか確率っぽいですよね。Neuralありますね。Dataとか。こんな感じで、この分野っぽい発表がやっぱりあるなと。

2つの学会の発表タイトルのキーワードを比較してみると、出てくる単語っていうのは、例えば1っていうのは出現回数が1回の単語が何個あったかということを表しています。1回しか出てない単語が多いなという特長はだいたいどちらも同じような感じですね。これは縦の軸が当然違うので、パーセントに直すと傾向としては一緒です。
時期的な流行りは大体同じで、1回しか出ないのは違うっていうのは、多分応用先が全然違うからということなんでしょうね。

ここからが数学の話ですね。またf(l.θ)という式が出てきたわけですけど、予測とかをやるときはいつでも何か関数を用いてやるとは限らないのですが、ここではこのような関数を考えるものとして話を進めます。
データを数値化するという部分と、あとパラメーターをどう設定するか? そもそも関数をどういうふうに考えるか? あと推定の方法も、点でやるのか? 区間でやるのか、Bayes的にやるのか? というようにいろんな方法があるわけですよね。
それはそうなんだけれども、今回は「データから特徴を数値化する」、この部分にスポットを当てたいと思います。

データ空間の作り方なんですけど、基本的にはユークリッド空間が考え易いですが、他にもいろんな考え方があります。例えばこれは、カイ二乗検定による特徴抽出と書きましたが、これはヒューマンコンピューターインタラクション研究会での発表ですね。カイ二乗検定を使った特徴抽出的なものもあります。
私は自分で、統計的検定を使うような感じの特徴抽出みたいなものをちょっと考えたのですけれども、それより前に同じような研究があったということで、ちょっと引っ張ってきました。データ間の微妙な差異を検定で測りたいというものです。
人間の試行の過程とは異なるかも知れませんが、人間がやっている特徴の切り出し方はデータの細かな差異を見ている感覚がありますから、統計的検定を使えば計算機にも人間の特徴抽出方法に近いものを取り入れることができるかなと思います。
代数統計って言葉は聞いたことがあるかないかわからないですけど、これに関する話をしてみます。難しいと言えば難しいんですが、これはやり慣れたらそんなに難しくないんですよ。数学を使うやつって大体そうなんで。何かのきっかけがあったら使う人が増えるのかなと思って、あえてやってみようと思います。
このスライドの内容について、今回の学会では私の学生が発表するんですけど、学生が発表する部分とちょっと絡めながら話を進めていきます。目Grepってさっき話をしましたね。バイナリに色付けすると。その特徴を見て、マルウエア解析とかされている人とかもいらっしゃるようです。
これを少しアカデミックな感じで考えると、計算機だったらもっと人間より精密に特徴抽出できるんじゃないか期待したいところですね。目Grepで人間ができるということは、計算機だったらもっと精密にできるんじゃないか? という期待です。

それでは代数統計の応用について話をしていきます。図の曲線はあるファイルの情報の特徴をユークリッド空間上の点として表したものです。16進数2桁の情報を考えているので256個のデータがあります。
ただし、目Grepをするときには少ない色の種類で、256次元のベクトルを16次元に圧縮して、そこから特徴抽出してみました。ここではプロットされた点に対して、フーリエ級数みたいなものを当てはめてました。
ここまでは特徴空間の話で、次は特徴空間上のデータについて遠いとか近いとかという概念について考えていくわけですね。ここでは分割表というものとを使って遠いとか近いとかを考えていきます。
分割表を考えることで、例えば甘い物好きと虫歯の関係といったことを統計的検定によって分析できるようになります。
分割表の独立性検定はカイ二乗検定がよく使われます。しかし、データを集めてみると、サンプル数がそんなに集まらないということもありますし、スパースっていって、0がすごく多い奴は、カイ二乗検定の時なんか、当てはまりが良くないとか、いろいろな話もあるんです。
そういう問題点があって、カイ二乗検定じゃなくてFisherの正確検定というのが考えられていて、そういうのを使うのが良いということも教科書的に書かれています。どっちでもいいやという人がいると思うんですが、そんなことを言ったら何も始まらないので、Fisherの正確法を使うことを考えてみます。
ところがFisherの正確法っていうのは、計算量的に困難な問題があってなかなか難しいのです。分割表の数え上げという問題があります。あとで説明します。それでFisherの正確検定を実行することは計算量的に難しい場合があるので、p値の計算を確率的にやろうとする枠組みとかがあったりするわけです。それが代数統計ですね。

サイズの小さな分割表を考えましょう。表にある3や6は周辺頻度と呼ばれていてここを固定する問題を考えます。10はトータルです。図のように、xに2を代入すると他の空欄が埋まります。ただし、空欄に入る数字は0より大きな整数です。
この分割表ではxに何か値を入れると他の空欄がすべて埋まるため自由度が1となります。数え上げというのは、この例ではxの値として条件(0より大きな整数が空欄に入る)を満たすものはいくつあるか数えることをいいます。図にあるMOVEというものを考えれば、ある分割表から他の分割表を作ることができ、MOVEをうまく構成できれば全ての分割表を列挙することができます。
このMOVEってやつなんですけれども。ここに代数的な話が入ってきます。これはDiaconis(ディアコニス)先生が、1998年に考えられた方法です。どれくらいメジャーなのか分からないですけど、面白い考え方だと思います。

2×2分割表を使って、分割表がどのように数学的に表現されるか見ていきましょう。分割表の周辺頻度の計算は行列を用いて表現することができます。この行列は縦に全部足すと2になっているので、原点を通らないある超平面に列ベクトル点が乗っているといえます。このような行列を配置行列と言います。ここまではそんなにむずかしくないですね。
次に、準同型写像は確率における「独立」という概念に対応していることが読み取れると思います。例えば、U₁₁はV₁∗V∗₁に対応させます。
この準同型写像の対応からスライドにあるイデアルを考え、グレブナー基底を計算することでMOVEを求められることが知られていて、これが、Diaconis先生たちがやられた仕事です。

2×2分割表の場合で具体的にどのような計算が行われているかをスライドに示します。この場合はf₁,f₂,f₃,f₄の4つの多項式(他の分割表でも二項式になります)のグレブナー基底を計算してu₁₁u₂₂-u₁₂u₂₁という多項式が得られます。この式からMOVEがどういう形のものか知ることができます。n×m×……という分割表ではこの計算は大変で、このような場合どのようなMOVEが存在するのかを求めることも研究対象です。
グレブナー基底を計算することは単純でスライドにあるように多項式の四則演算を行っているだけです。
しかし、考える多項式の個数がたくさんある場合は、グレブナー基底を求めるための計算手続きの量が増えるため、ここにこの問題の難しさがあるわけです。
なんかおっかない話をしているように見えるかもしれませんけれども、さっきの準同型写像が、分割表の中身(2,1,4,3)の部分と周辺頻度(3,7,6,4)を対応づけていることを確認することは簡単です。単項式u₁₁² u₁₂¹u₂₁⁴ u₂₂³の指数部分2,1,4,3が分割表の中身であるセルの部分に対応しています。指数部分の2,1,4,3は分割表の中身に対応しています。
準同型写像の計算を進めていくと単項式v₁∗³ v₂∗⁷ v∗₁⁶ v∗₂⁴が得られ、この式から分割表の周辺頻度が3,7,6,4であることに対応していることが分かります。マルコフ基底について、この準同型写像の計算をすると0となり、これは周辺頻度を変えないということに対応することも分かります。
という具合に、実際にどのような作業をすれば良いかということを理解できればそんなに難しいものではないと思います。みなさんなら少し練習すればこのような理論を使いこなすことは難しくないでしょう。そしてどういうものにこのような理論が使えるか考えて欲しいと思います。

今までは2×2分割表を考えて来ましたが、ルービックキューブのようなものを考えるともっと色んな分割表を考えることができますね。分割表が大きくなっていくとMOVEもどんどん複雑になっていきます。
分割表が巨大(多次元)になるとその数え上げも難しくなり、独立性検定に必要なp値の計算が困難になります。しかし、考えたい分割表のマルコフ基底さえ求められれば、分割表を全て数え上げる代わりに、MOVEを利用した分割表のランダムサンプリングが可能となり、MCMC(マルコフ連鎖モンテカルロ法)を用いてp値の近似計算をするというような方法が提案されています。

マルコフ基底がどのように導出されるかについては、少し大変ですが具体的に手計算をすると良くわかります。当然といえば当然ですが、ある形のマルコフ基底を求めるときには、はじめにどのようなS多項式を計算するかということが重要です。グレブナー基底に関する知識があれば、2×2分割表を考えたときの4つの多項式のうち、f₁とf₄についてはS多項式を考える必要がないことは分かると思います。

多分そろそろ時間なので、一般的な目Grepについて紹介します。これは、EXEファイルなんですけれども、同じEXEファイルでも、個々のファイルによって着色の具合が異なることが分かると思います。このような中でも微妙な特徴の違いを目Grepのプロ達は見いだしているのだと思います。

そういうわけで「着色による可視化」という方法で、素人向けには「エキスパートは特徴をどう捉えているか」ということを伝えることを目的とし、エキスパート向けには「作業の支援」を実現することを目的として研究しています。まだちょっと時間があるみたいなんですけれども、以上で終わりたいと思います。質問がある方は来てください。どうもありがとうございました。
 リクルートが主催する「情報処理祭」は、情報技術を学ぶ学生を対象に、自分の知識が実際の社会や企業でどう使われているかや、情報処理分野の最新動向を横断的に学べるイベントです。 ・公式サイト
リクルートが主催する「情報処理祭」は、情報技術を学ぶ学生を対象に、自分の知識が実際の社会や企業でどう使われているかや、情報処理分野の最新動向を横断的に学べるイベントです。 ・公式サイト続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします