 PR
PR2026.02.26
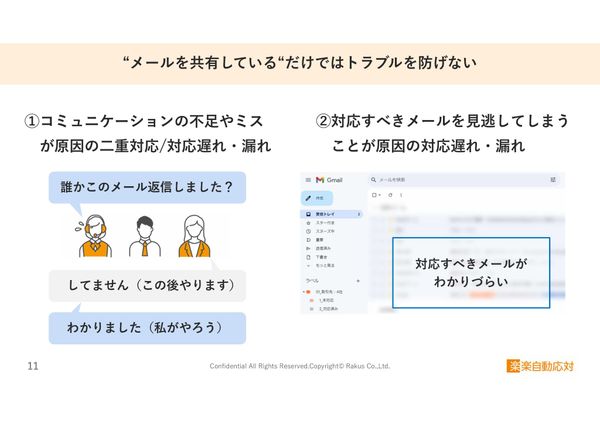
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
自由研究・テイラー展開(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏(以下、安原):Unityの安原です。今回で微分積分のお話は一段落になるんですけれども、最後は僕の自由研究みたいな話をちょっとおもしろおかしくしてみたいと思います。

微分積分ってすごくおもしろい概念で、応用がメチャクチャ広いんですよね。微分積分がなかったらいろいろなものが生まれてきていないのですが、その中に「テイラー展開」というものがあるんですよ。
これを見てください。これはWikipediaに書いてある内容です。ちょっと難しげに書いてあるじゃないですか。これを説明してみましょう。

これがテイラー展開、テイラー級数と呼ばれるものです。このΣは、「Σの後ろを、nを0から無限大まで変えていきながら全部足していきますよ」という記号です。

この「!」は階乗です。nが3だったら3×2×1、4だったら4×3×2×1みたいに階段状に全部掛けていくものを指します。nがものすごく大きくなると、すごい勢いで大きくなっていく数字ですね。このfのaのカッコにnがありますが、これはn乗ではなくて、n回微分しているという意味です。「このプライムの数がn個あるよ」ということですね。

ここは、x−aのn乗で、aというのは定数になります。これは、aのポイントに注目しているという意味になるので、aは定数ですが、ここに0を入れるとこうなります。

ちょっとシンプルになりました。aはいくつでも成立するので、0でも成立します。0のことを「マクローリン展開」と呼ぶらしいです。テイラー展開の1つですね。


無限に微分できるという前提があると、あらゆる関数がxの……1足すxの2乗足すxの3乗足す……が表せちゃうよと、けっこう大胆なすごいことを言っているんですね。三角関数でも成り立っちゃうというのがけっこうびっくりするところです。


安原:例えばサインカーブのsin xで考えてみましょうか。このマクローリン展開を計算するために、こういう表を作って中を埋めていきましょう。
nが0の時、0回微分、つまり微分しない状態ですね。これはsin x。1回微分するとcos x。それを微分すると、こういうふうになります。

ここのxに0を入れたらどうなるかというと、sin 0は0、cos 0は1。sinのところは全部0ですね。cosのところは1が入って、ここは−1。こうなりますね。


0の階乗って1なんですよ。1の階乗も1です。3の階乗は3×2なので6。24、120、720、5040となる。xのn乗は……となるので、本当は無限にやらなきゃいけないんですが、7までにすると、この式はsinは0なので、cosだけを考えればいいですね。


ということになります。これももちろんずっと続くのですが、例えばここで切ってやめてみるとどんなグラフになっているか見てみましょう。

これがsin x、普通のサインカーブのグラフですね。

このグラフは先ほど計算した7までやったところです。見てください、メチャクチャ近い値が出ています。3の近くでようやくズレ始めるんですが、0付近は完璧に同じサインカーブに沿っています。これをずっと続けていくと、無限にサインカーブに近づいていくという、すごいことを見つける人がいるもんだなと思います。

安原:これを踏まえて、こんなデモを見てみてください。例えば、動いているのが敵の飛行機だとしましょう。四角いものが左下に見えていますね。これが砲台だったとしましょう。ここから大砲を撃つ。このニョロニョロ動き回っている、回避運動をしている敵に大砲を当てられるか。
重力があるのでもちろん放物線を描くのですが、これを当てるのはけっこう大変ですよね。ここで動いているものに対して、ちょっと前の状態を使うと微分値が出せるという理屈があるじゃないですか。これを使って何回か微分して、ここの値から未来を予測できるんじゃないのかと僕は思ったんですね。


この理屈を使って、ここの点の微分値に注目、つまりここでテイラー展開をしてあげれば、ここの関数が見えるから、ここが見えるんじゃないかとやってみたのが次の動画です。


2回微分したものが緑のポイントで、3回微分したのが水色ですね。当たった時に点数が加算されるようになっています。当たる時刻もわかるので、当たると予想された時刻で炸裂して赤くなるようにしています。
より敵に当たるかと思うのですが、どうですかね。これがなかなか難しくて、これを4回微分するとぜんぜん当たらなかったんですけれども、3回微分だと2回微分よりは成績がいいです。数字が右上に出ていますが、「third」というのが3回微分ですね。3回微分のほうが何回かやっていると成績がいいことがわかるので、「まあ、やった甲斐はあったかな」みたいな話になります。
微分は、ちょっとしたズレですごく大きな影響を与えるので、誤差があると壊滅的になっちゃうんですね。たまにぜんぜん違うところに大砲を撃っちゃったりするので、こんな難しさはあります。
というわけで、このテイラー展開の理屈を使ってなにかできないかなと思ってやってみました。もっとバッチリ当たるかなと思ったんですけれども、なかなかそうはいかなかったので、あまりかっこよくないんですけども(笑)。ちょっとおもしろいデモだったのではないでしょうか。

このテイラー展開もすごく役に立ちますし、三角関数がこうやって級数で近似できるということを知っておくと、プログラムでもけっこう役に立ちます。
というわけで、微分積分について4回にわたって動画を作ってみましたが、いかがでしたか? ちょっと使えるようになったなと思ってもらえたら幸いだなと思います。ぜひUnityでプログラムを組んで素敵なアプリケーションを作っていきましょう。以上です。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします