 PR
PR2026.02.26
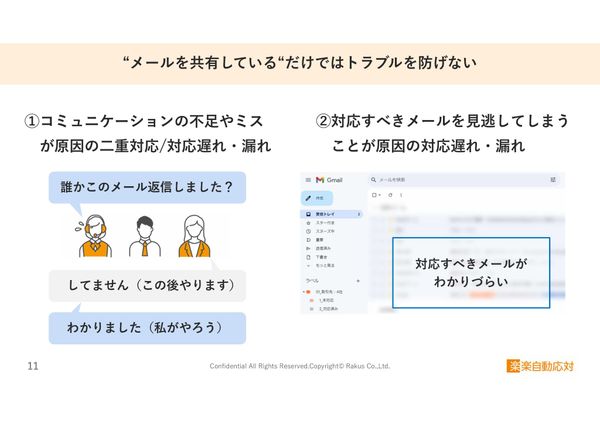
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
積分は面積(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏:Unityの安原です。今回は積分についてお話ししていきましょう。

数学をやっていると時々、すごく不思議なことに出会ったりするんですね。「なんでだろう、これ」と思うようなことがあるんですよ。積分をやっていると特にそういうことに出会ってくるので、今回もそういう話をしていきたいと思います。楽しみにしてください。
まず積分について簡単に説明してから、プログラムでどう扱っていくのかを話していきましょう。では積分の説明からいってみましょう。
はい、こんなグラフがあったとしましょう。y=f(x)という関数があって、ある点に注目して、この傾きに注目するのが微分でした。では積分はなんなのかというと、この面積に注目するのが積分です。


ちょっと具体例から見てみましょうか。これはすごく単純なグラフで、y=2xのグラフです。1のところは、2xなので2になります。この面積はいくつなのかといったら、x=1で、y=2で、1掛け2の半分だから、1ですね。ここに書いときましょう。面積は1です。


このx=2のところは、y=4ですね。この三角形の面積は、2掛ける4の半分だから4ですね。実はこの数字の2乗が面積になっているんですよ。2の2乗が4なので、3のところは9になるはずですね。ここが1の2乗、2の2乗、3の2乗。これはずっと同じように続いていきます。

なのでこのy=2xの直線の面積は、xの2乗になります。これを記号で書くと「∫」。インテグラルと読みます。積分の記号ですね。

dxというのは、xで積分するという意味です。そうするとx^2+c(※xの2乗)は、Cという定数が付くのですが、xの2乗になるよというのが積分です。

前回の微分の時の、xの2乗の微分が2xになるという話を覚えているでしょうか。ちょうど微分と積分は反対の関係になっています。
これは前回説明した図なのですが、xの2乗、2xになるよという話をしましたね? 積分はこの反対というのがおもしろいところで、微分と積分はこのように対になっているんですね。
ちょっと注意しなきゃいけないのは、この定数のところです。前回は123という数字で説明しましたが、なんらかの数字は必ずゼロになっちゃう。ということは、ゼロを積分するとなにかの定数Cが生まれてくるよという話になるので、このCが生まれてきているということになります。


積分は2種類、不定積分と定積分というものがあります。これは不定積分です。不定積分は、結果が関数のかたちで現れます。ここにxが入っているということですね。
では定積分はなにかというと、定積分は値で出てきます。定積分をこの図で説明しましょう。ここからここまでというエリアを確定させると、結果は関数ではなくて値になります。100とか200とか、そういう値になる。これを定積分といいます。


積分について、ちょっとおもしろい話に踏み込んでみましょう。(式を示して)こんな積分があったとしましょう。この0、1というのが付いていると、定積分の意味になります。つまり、ここからここまでだよというのが、0から1までだよという意味になります。この定積分の答えは1つの値になりますが、これはなにか? という話です。

もしかしたらご存じの方もいるかもしれませんが、これはとてもおもしろい結果になります。答えを言いますと、π(パイ)です。円周率ですね、3.141592という値になるんです。

ちょっとグラフを描いてみましょうか。ざっくりですが、4割る1+xの2乗の曲線の0から1までの面積が、円周率になることを意味しています。どうですか。けっこう不思議で、おもしろいですよね。

これをプログラムでやってみましょう。どういう考え方でこれをプログラムに実行させるか。ある細い区間を、dxとしましょう。dxと高さを掛けると、この細い部分の面積が出るじゃないですか。これを全部(曲線の0から1までの面積分)足す、というのが積分の計算方法になります。

ではプログラムを見てみましょう。SharpLabですね。微分の時もやりましたが、このサイトでやってみましょう。まず余計なところを消してからやっていきましょうか。
まず、なにか適当な数字を出してみましょう。100を書いてみると、右側に100が出ます。はい、実行されてるぞと。では先ほどの関数をそのまま書いてみましょう。funcで、引数はxで、中になにを書くかというと、この式ですね。4割る1+xの2乗という式をここに書いておきます。この積分が欲しかったから、まずその中の式だけを書いちゃいます。


とりあえずこれを実験で呼んでみましょうか。r=func、いくつにしましょうか。なにか数字を入れましょう。10を入れてみましょうか。結果は、ここにrを入れると右側に出ますね。0.03。このような数字になりました。

ここから積分の計算をしていきましょう。まずrを0にする。これが大事です。そのあと、FORループを書きます。xは0で、xが1まで。これが定積分の0から1までを意味しています。
それで、dx。小さな値を定義しておきましょう。例えば0.1とかにして、このxをdx分だけ増やしていくというFORループにします。ここが大事なのですが、+=なのですね。r+=でfuncにします。
ここで大事なのが、ここです。dxを掛ける必要があります。そうすると細い部分の面積になるので、はい、これがΠになっているかどうか。ちょっと右側を見てください。3.2399。けっこう円周率の3.14に近い値になっていると思いませんか。ちゃんとできているのがわかるんですね。

この0.1をもっと小さくしたら、より3.14に近づくのではないか。0.01。はい、3.17。いいですねぇ。こんなふうに小さくすると、ちゃんと3.14に近づいていくんですね。

このSharpLabのサイトは、ループ数の制限があるのでこれ以上はちょっといけないのですが、精密な円周率が出てくるのを見るとすごくおもしろいので、みなさんもぜひUnityとかですごく小さな値をここに入れて、やってみてください。
そんなわけで、積分はなかなかおもしろいと思いませんか。次は、Unityでゲームを作る時に参考になるようなデモを見てみましょう。
Unityを開いて、zakoというのを表示させましょう。これはザコ敵ですね、ザコキャラに対して、Zako、Z・a・k・oというスクリプトを新しく作って足しました。中はどうなってるかというと、こんな感じです。
Updateの中は、ポジションをいじるプログラムにしましょう。x座標に三角関数、Sin(Time)を書いておきましょう。その上で、振幅を10とかにしておきましょうか。そして10を掛けておく。これでですね、Sinカーブを描くザコキャラが作れました。

さぁこれを実行してみましょう。どうでしょうか。はい、これがSinカーブになります。非常に単純なプログラムですが、Sinカーブを描く敵ができました。
これを複製して、もう1個別のプログラムを付けてみましょう。さっきのプログラムは消してから、新しいプログラムを足します。Zako(1)にしましょうか。
このプログラムを編集します。先ほどのZakoのプログラムを丸ごとコピーしてからやりましょうか。ここにコピーしてから、class名をZako1にしておきましょう。はい、これは先ほどのプログラムそのままなのですが、ここですね、+=にして、SinをCosにする。そして、deltaTimeを掛ける。

これは、Sinを微分するとCosだったので、それを積分したら元と同じになるでしょうという理屈ですね。つまり、このプログラムはさっきと同じ動きをするはずです。本当でしょうか。はい、このとおり。ちょっと誤差がある気もしますが、同じ動きをしているのがわかるでしょう。
次は、Zako(2)というプログラムを作ってみましょう。また複製して、1つ下に作りました。さっきのプログラムは消してから、新しいプログラムZako(2)にしましょう。
新規で作ったら、これも先ほどのZako(1)をまるっとコピーしてきましょうか。丸ごとコピーして、Zako(1)だった名前を(2)に変えます。今度はなにをするかというと、変数を用意します。ベクトルで。Vector3で、p1とかにしましょうか。
初期化しておきます。Start()でp1.xをLENにしておきましょう。10が入っていた数値ですね。先ほどは1回微分を積分したのですが、ここではさらにもう1回微分したものを積分します。ちょっと言葉の意味がややこしいんですが、ここに、Cosを微分したものということで、−Sinを書きます。

そうすると2回微分したものがここにあることになります。それを足し算していくと積分したことになるので、その積分した結果、p1をさらに積分するためにp1.xにすると、やはりこれも同じ動きをするはずです。2回微分したものを2回積分しているので、同じになるはずです。

では見てみましょう。はい、ちゃんと同じ動きをしているじゃないですか。
ちょっと複雑になってきましたが、おもしろいのは次です。また複製して同じように4つ目が生まれました。同様にプログラムを新しく作ってみましょう。今度はZako(3)にしましょうか。
作ったら開いて、やはりZako(2)を丸ごとコピーしてZako(3)にペーストして名前を(3)に変えましょう。よく見てもらいたいのは、ここのSin。Mathf.Sinのところは、最初のプログラムに戻ってみると、pos.xと同じ値だと言っているんですね。


同じ動きをしていたということは、pos.xと同じ値が入っているはずじゃないですか。なのでこのpos.xを、Zako(3)のほうに、これ(Mathf.Sin(Time.time)*LEN)の代わりにpos.xをポイッと置いちゃうんですね。これでも動きは変わらないはずということで、実行してみましょう。

さあ、どうなるでしょうか。全部同じ動きをするはず……はい、ちゃんとなっていますね。
それで、このZako(3)のプログラムをもう1度よく見てください。三角関数の技術が完全に消滅しています。deltaTimeを掛けたりはしているけれど、もう足し算をしているだけ、もうそれだけでSinカーブが描けてしまうという、この不思議な感じ。これもまた積分のおもしろいところだと思うんですが、Sinカーブはこういう感じで書けちゃうんです。

y座標に関しても同じようなものを作ると、こういうふうに円運動をするけれど、中にはSinもCosも書いていませんよというプログラムが書けてしまう、というわけです。これ、なかなかおもしろいと思いませんか。
これをどういうふうにゲームに使っていくか。物理的に意味を言うと、これはバネの運動に相当します。なので、それを使ったデモを見てみましょう。
例えばシューティングゲームで、敵がこう並んで出てくるゲームがあるじゃないですか。いかにも殺してくれと言わんばかりに、敵の編隊がこう並んで出てきます。
こういうの動きを作るのはけっこう面倒ですが、このバネの中心を定期的に動かして、あとは先ほどの積分の式を書くだけで、こういう滑らかな動きをしながら目標地点に向かっていくような動きを作ることができます。
ちょっとこのプログラムを見てみましょう。どうなっているでしょうか。
はい、こんな感じですね。−pos.xのところで、target引くposにしているんですね。それで、4fというのはバネ係数に相当します。その次の行が、dragに相当する速度比例抵抗を掛けています。こういう工夫をしておくと、先ほどのような動きができて、ターゲットの動きはルーティンで2秒おきにヒョイヒョイと動いているだけ、となります。


これは、工学的にはフィードバック応答といいます。微分方程式を習えば、なんでもない式から突然三角関数が出てくるということも数式的に説明できるんですが、プログラムだとより簡単にこういうことができて、なかなかおもしろいなと思います。
僕はシューティングゲーム作る時に、敵の動きをこういうふうに作ります。これも少ないデータでけっこう好きに敵を動かせるので、便利な機能です。ぜひ使ってみてください。
というわけで、積分の話はここまででした。どうですか、なかなかおもしろい話だったと思います。それに、そんなに難しい話もしていないと思います。プログラムで理解すると、積分もそんなに難しくないということがわかってもらえるんじゃないでしょうか。

ぜひみなさんも、Unityのプログラムで積分を使ってゲーム・アプリケーションを作ってみてください。以上です。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします