 PR
PR2026.01.19
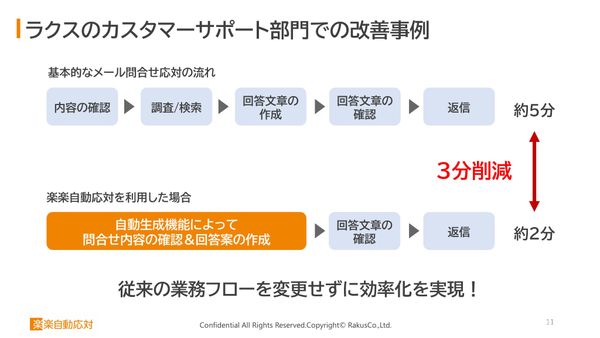
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
浮動小数点数(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏(以下、安原):パート4です。大丈夫ですか。寝ていませんか? パート4を始めていきたいと思います。浮動小数点数、floatです。

簡単な問題を出してみましょう。float aに「1f」を入れた時に、Debug.Logでそのaを出力させたらConsoleに何が出ますか? 急に聞かれると困るかもしれませんが、これは引っかけ問題ではなくて「1」が出ます。


次ですね、「1/3」。1割る3を書いたら何になるかな。これはちょっと引っかけ問題かもしれないですね。「0」になります。これは大した話ではありませんが、1f割る3fと書けば0.333になりますが、1割る3だと切り捨てられちゃうよという、わりとどうでもいい話です。

次です。「3e-1f」と書いてあります。これ、わかりますか。これはもう知っているか知らないかだけなのですが、こういうふうに書いても、きちんとコンパイルは通るし理解されます。この答えは「0.3」です。ぜひこれはお家に帰ってやってみてもらいたいですね。


どういうことかというと、eというのが数字の後ろに急に出てきたら、その後ろの数が10のべき乗を掛けていることになるよ、という話です。これは覚えておいたほうがいいでしょうね。2や、ネイピア数ではなく、10です。

という話がありつつ、floatの話をしていきます。ちょっとゴチャゴチャした話になりますが、floatは32bitあって、中身はこうなっているんですね。これは調べるとネット上にいくらでもある情報ですが、符号が1bitあって、指数部が8bitあって、仮数部が23bitあります。
ざっくり言うと、仮数部に2の指数部乗を掛けたもののプラスマイナスが結果になります。


実はこれはちょっと嘘で、(スライドを示して)厳密に言うとこうですね。1.0をベースにしていて、指数部からは127を引いて掛けるというのが、規格上の決まりごとになっています。

なので今001111と書いてありますが、これは、この上の32bitでfloatにした時に、ちょうど1.0を表現できるビットパターンになっています。これはベテランプログラマーはわりと知っていますが、16進でいうと、3f800がfloatの1.0です。
ちょっと限界を探ってみましょう。まず指数部。指数部は規格上、マイナス126からプラス127までいけます。では、2の127がどのくらいの数字なのかと計算してみると、長い数字の後ろのほうにeと書いています。つまり、10の38乗を掛けている。

パート3で対数の話をした時に、だいたい3分の1と3倍の関係という話をしましたが、127の3分の1はだいたい38じゃないですか。これもだいたい合っているんですね。
けっこう大きな値ですね。小さいほうはどれくらいかというと、eのマイナス38乗、つまり10のマイナス38乗というすごく広い値です。

floatには限界があるということをなんとなく知っている方は多いと思います。ですが、実は表現の幅は超絶広いです。どのくらい広いかというと、これはちょっとお遊びで調べてみたのですが、10の36乗を表す、澗(かん)という単位があります。なので、100澗ぐらいの数字が限界になるわけです。この値まで使うことはあり得ないぐらいの大きな値を扱うことができます。

では、小さいほう。調べても調べても、10のマイナス24乗以下の単位が見つかりませんでした。誰か教えてほしいのですが、涅槃寂静(ねはんじゃくじょう)という尊い感じの単位があって、これでもまだ10のマイナス24乗です。なので、マイナス38乗どんだけだよというぐらい小さな値を表現できます。
また、一番下に小さく書きましたが、僕の知識の中で一番小さな物理定数を考えると、ディラック定数というものがあります。10のマイナス34乗なので、これでもぜんぜん大きいですね。

というぐらい小さな値を、実はfloatは表現できます。
ですが、やはり限界はあります。どこに限界があるかというと、むしろこの大きいほうのここです。23bitのほう。つまり大きな数字に小さな数字が足されている場合、表現できないということになります。
例えば(スライドの)下に書いてある、1,000万にすごく小さな値を足すことは、floatでは表現できません。

では、この23bitのほうをちょっと深掘りしてみましょう。この仮数部は、2のマイナス23乗という小さな値を扱えると主張していて、どのくらいの値なのか見てみると、このくらいになります。

1.0に足せる最小の数。floatのビットパターンの一番右側に1を立てて表示させるとこんなふうになります。このぐらいの値が限界ということになります。
1と、この小さな桁が始まるまでの距離は7桁ぐらいです。これも計算するとわりとわかるのですが、log10の2というのは0.3なので、23bitにこの数字を掛けると6.9という値が出てきます。なので、だいたい7桁というのが計算上もわかってくるわけです。


具体的にまずいところへ近づいていきましょうか。(スライドの)一番上ですね、10という数字に一番小さなbitを立てた時はこのぐらいです。100、1,000といって、10,000になった時に0.0009。これが一番小さな単位、解像度です。分解能と言いますが、そういう値になるわけです。

例えばUnityでトランスフォームに値を入れていたとしましょう。原点から10キロ離れたところでなにが起きているかというと、1ミリの分解能が限界になっているわけです。1ミリと1ミリの間、つまり0.5ミリみたいな値を表現できなくなっているということになります。10キロ離れるのはそんなにないかもしれませんが、これは知っておいたほうがよいでしょう。

もっとヤバいのは時間ですね。例えば1.0を1秒にするケースは多いと思いますが、そうすると24時間で86,400秒になるんですね。この状態でどのくらい小さな値が使えるのかというと、計算してみると7.8ミリぐらいが限界になります。
例えば、プログラム上で毎フレームdeltaTimeを足している部分があったとしましょう。24時間これを回していると、16ミリ秒足しているつもりでも分解能が7.8ミリになってしまうので、15ミリしか足されていないみたいな、おかしなことが起きてしまいます。これは明らかにおかしなことが起きるので、気をつけましょう。

実際ヤバいのは知っていても、具体的にどのくらいなのかというのは意外と知らない方が多いと思います。具体的に知っていると、嗅覚が働くというか、「これはヤバいんじゃない?」というのがわかってきます。
そういう問題にぶち当たってから調べるよりもやはり効率はよいので、このへんは知識として知っておくと制作に役立つかなと思います。
ちょっと実験です。原点からzの値をガンガンガンガン足してみました。まだけっこう大丈夫ですが、Standard Shaderで普通に出している男の子がだんだん、だんだん人の形を保てなくなっていくのがわかるでしょうか。
(会場笑)


900キロ離すとかはゲームではちょっとあり得ないと思いますが、ええーヤバい。ヤバい(笑)。ヤバいですね、これは本当にヤバいことがあります。

みなさん、こんなのやらないだろうと思うかもしれませんが、マップゲームとか考えてみてくださいよ。同じアプリで東京とロンドンの家を表現する時に、人によってはずーっと画面を見ていて、連続しているかもしれないですよね。その時にどう対応するのかみたいな、おもしろいですね。
もう人の形を保てなくなっていますが、マップゲームの場合だと、いろいろな対応はあると思いますが、例えば1キロなら1キロで原点に全体をずらすという処理がおそらく必要になるでしょう。

これはなんにも考えずにやった場合で、絶対こうなると考えるのは誤解があります。なので、ちょっとシェーダーを入れ替えます。右側の男の子は、がんばって姿勢を崩さないように僕がシェーダーを書いてみたものです。左側は先ほどと同じですね。
右側の男の子は崩れないのですが、結局シェーダーでがんばっても、アニメーションの部分の精度が落ちるので、首がガクガク動いたりして、結局駄目なのですね。こういう対応をしてもあまり意味はなくて、今は影を出していませんが、影を出すともっとヤバかったりします。ここをシェーダーでがんばる意味はほとんどないです。気をつけましょうという話になります。


おもしろいので、ぜひやってみてください。簡単にできます。トランスフォームのzの値を、ずっと足すだけです。
もう1つやり方があって、double(double precision floating point number)ですね。doubleを推奨したい。先ほど、時間の例がありましたね。86,400という数字があった時に、doubleだったらどうなるかというと、仮数部は52bitなので、24時間経っても0.014ナノ秒までいけます。かなり強力。365日ずーっとアプリを動かし続けても3.7ナノ秒までいけるので、doubleはほとんど無敵に近いですね。

もちろん、毎フレーム300足すとか、もっとヤバいケースがあるかもしれませんが、doubleにしておくと特に時間に関しては大丈夫です。
なので、僕はずっと足していくTimeとかをやる時は、だいたいdoubleを使うようにしています。doubleが遅いかというと、実は計算上はそんなに遅いわけではなくて、現代のプロセッサーだとぜんぜん遅くありません。むしろdoubleのほうが速いプロセッサーもあるぐらいなので、double使っていきましょう。
というわけでパート4が終わりました。floatの限界を具体的に知ってみようという、実験をやってみました。2進数と10進数の桁の関係がわかると、このへんの勘も働くでしょう。このあと公開しますが、ここについてもうちょっと詳しくブログを書いたので、興味ある方はぜひ見てください。というわけで、パート4は終わりです。

続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします