 PR
PR2026.01.19
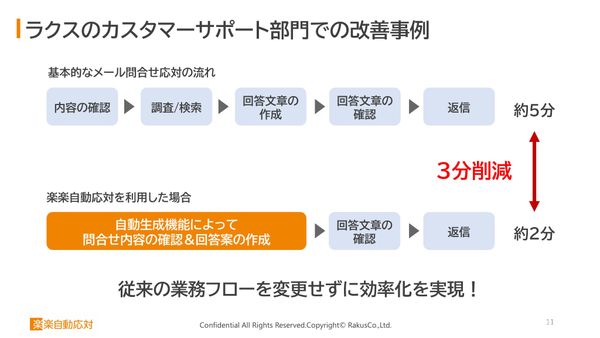
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
式の読みかた(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏(以下、安原):次はパート2ですね。ここではかなりフワッとした話をします。数学の話をする時は、どれだけ間違ったことを言わないかと気をつけなければならないので本当に大変なんですが、ここは本当にフワッとした情緒的な話をしていきたいと思います。そのほうがわかりやすいことも多いかと思うので、お話として聞いてみてください。

これはマサチューセッツ工科大学の購買部で売っているTシャツで、僕の同僚が買ってきてくれたお土産です。これがグッズとして売られているということは、あえて「これ、わからないでしょ? ハハハ(笑)」という、いやらしい感じで、数学や物理が好きな人はこういうのが好きですよね。
ペダンティック(pedantic)な感じの、いやらしい感じのTシャツなわけです。これを見て「うわー……」となるのが普通の人です。ちょっと書き起こしてみるとこんな感じになるかな。わからないんですけどね。「これわからないでしょ? ハハハ(笑)」という、そういうアイテムなので、わからなくて当然なわけです。


数式を見ると、コンマ1秒で目を逸らす人が大半だと思いますが、このパート2ではその時間をどうにか3秒まで伸ばしたいと(思っています)。
(会場笑)
まず式を見た時に、どこから見ていくかという話です。足し算と引き算は逆の考え方なので反対かなと思うかもしれませんが、実は意味はほとんど同じです。なんでかというと、(スライドを示して)今bを足しているのとbを引いている式があるのですが、例えばこれが物理の話だとすると、bが暑さだったらプラスだけど、寒さだったらプラスのほうが寒いとかあるじゃないですか。
決め方によってマイナスかプラスかは変わってしまう。単にそれだけの話になってしまうので、ここに目を奪われる必要はないんですね。でもaとbはプラスとマイナスのどちらかで分離されているということを意識する必要があります。

次に掛け算と割り算。これはやはり足し算とは違って、塊として見るのが正しいです。これは次の話を交えて説明をしていきましょう。複雑な数式があった時に、掛け算・割り算のグループが足し算あるいはイコールでつながっていると。ここに分離があると考えるのが、とりあえず式の見方としては進んでいけます。ちょっとは見ていられるようになります。


というのも、等号があった場合、必ず左右で単位は等しいじゃないですか。aが秒だったらbも秒ですよね。aが距離だったらbも距離。これは間違いないじゃないですか。これが足し算と引き算であっても、やはり単位は維持されるわけです。

今こういうa+b=cという式があったとして、こう変形したとしましょう。ここで最後に=0が書いてあると、「0なのか」と、わりとそこに意識が引きずられると思うんですよ。ですが、実はそこに意味はないんですね。単なる変形で、その0は生まれてきちゃうわけなので、今1番目の式と2番目の式でまったく意味が同じなのはわかるでしょうか。ただの変形なので、その0に意識を持っていかれる必要はないんです。そこを見る必要はなくて、結局足し算と引き算で分離されているということを意識しましょう。

なので、先ほども少し触れましたが、単位が異なるものというのはイコールの左右にもいかないし、足し算に足すことも絶対にできないわけですよ。メートルと秒を足すということは絶対にありえないので、ここで意味が区切られていると見るのが1つの見方になるわけです。

さらにもう少し見ていこうとした時に、なにか1個に注目するのがコツです。例えばdに注目するとします。その時にdが増えたらこの塊は増えますよね。でもeが増えたらこの塊は減っていきますよね。そういう関係を考えると、式を見ている時間が少し長くなります。

dの話をもう少ししてみましょうか。ではd以外の値が固定だとしましょう。a、b、c、eまでが固定だったとして、dとfgの関係になると、これは式でf(x)=ab+cx/eという関数になるので、これでもうけっこう複雑さは減っていると思うんです。そんなに難しくないという話になります。

先ほど式が4つあったのですが、その中の一番面倒くさそうなやつをここにもう1回出してみました。どうでしょうか。足し算が見えますか? ありますよね。単位がイコールの左側に1個と、足し算の両側に1個ずつあるから全部で3つの塊があって、その3つの塊は単位が同じだということがわかります。記号の意味がわからないのを何も恥じることはありません。ただ知らないだけなので、それは教えてもらえばいいだけです。

例えばここで言うと、Jは電流です。そして、Bは磁束密度です。それは調べればいいだけの話で、あとはこの式を見れば関係性がなんとなく見えてくる。もちろん∫(※インテグラル)という記号がよくわからないなとかあるかもしれませんが、傾向は見えてくると思います。これでたぶん3秒ぐらい見られるようになったんじゃないかなと思います。
もう1つ説明として追加したいのが、漸化式というのがあるよという話ですね。左側にn+1みたいな記号があって、右側にnという記号があった場合にこれを漸化式といいます。これは通常の式とはけっこう異なるんです。必ず初期値があって、例えばa0=0みたいな式があって、an+1=an+2n+1みたいな漸化式があるわけです。

これはプログラムを書いている人にとっては何のことはないんですね。例えば、Update関数というのは、毎フレーム呼ばれますよね。その外側にaというのが宣言してあったとして、a+=1みたいなことを書くじゃないですか。これは漸化式なんですよね。前のaに新しいaは1を加えてあげるよというだけなので。なので漸化式のほうがプログラミングと親和性が高いんです。

漸化式についてもう1回さっきの例を出すと、上の2行の式が漸化式の定義になるわけです。具体的にa1はいくつかなと考えた時に計算できますよね。a1、a2、a3の計算ができていきます。計算するとa1というのはa0に1を足したものだなと。だからa0は0だから1だねと。今(スライドに)ピンク色で出ているのが結果ですね。1、4、9となっていくわけです。

この右側にaを使わない形式で表現できたらある意味勝利なんですよ。一般項と呼ばれるもので、もうこうなってしまえばいきなりa1,000とかが求められるという強さがあるわけですね。nの2乗になるのはちょっとおもしろいと思いませんか?

ちょっと余談ですが、前の値に奇数を足すと2乗になるというおもしろい数字の性質があって、これはなんでだろう? みたいな感じで悩むとちょっとおもしろいですよね。ちょっとヒントというか違う視点を見てみます。今右側に小さい点を書いていますが、前の値に奇数を足すということは正方形を大きくしていく操作に他ならないわけなので、2乗になるんですね。

こういうのを見るとなるほどと思うかもしれません。同じことを言っているんですが、数学はこういうふうにちょっと見方を変えると「なるほど」と思ったり思わなかったりするので、なるほどが増えていくとおもしろいですよね。これは余談でした。
というわけで、パート2はここまでになります。まとめとしては、足し算引き算および等号で分離されているということに注目していきましょうねと。物理の話に限定されますが、必ず単位があるのでそこを意識しましょう。そして、漸化式というのがあるよという話でした。パート2はここまでになります。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします