 PR
PR2026.01.19
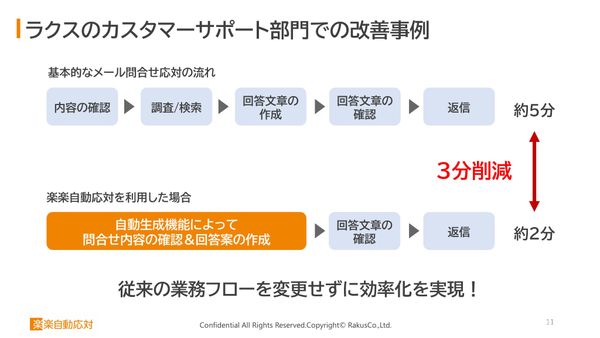
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
数式とグラフ(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
安原祐二氏:Part1です。「数式とグラフ」というタイトルを付けました。まず、Part8まで行く前に、このおさらいをさせてください。これ見ていただいて、どうかな。どうお思いでしょうか? パッとこれが何のことかわかる方と、「あれなんだっけな」「これどうなったんだっけな」と思う方と、「ダメ、全然わからん」という3通りの方がいると思います。

僕の勘ですが、ここに来ている半分ぐらいの方は、「ちょっとわかんない気がするけど、たぶんあれだな」ぐらいの感覚を持っているんじゃないかなと思っています。具体的な数値がどうこうではなくて、この意味がわかるかですね。そのぐらいの方が、たぶん僕のPart1から8までのお話がしっくりくるというか、なるほどと思ってもらえるんじゃないかなと思います。
これがもし、「全然わからん」「ダメです、すみません」という方は、ちょっと難しいかもしれないので、今日は雰囲気だけ持ち帰ってもらって、これをちょっと復習してもらいたいと思います。これがわかるだけではなくて、例えば「1/2乗」と「−2乗」のどちらが大きいかをパッと答えられたり、「3/2乗」はどうだったかなとか、そのあたりもパッとわかるようになると、今日のお話はすごくわかりやすく聞けるかなと思います。
「これはわかるよ」という方もいるでしょう。「何これ?簡単だよ」という方は、どちらかというと教える側の立場の人だと思うので、得るものが何もなかったなと思うのではなくて、人への伝え方をともに学んでいきたいですね。俺だったらこういう言い方じゃなくて、こう言うなという視点でこの講演を見てもらえればと思います。
一応、答えを出しておきましょうか。こんな感じですね。大丈夫ですか? 「1/2乗」っていうのは「√」ですね。キツい? 大丈夫?(笑)
(一同笑)

こんな感じになります。指数がいくつであっても、0より小さくはならないというところは、確実に押さえておかなきゃいけないポイントかなと思います。
では数式とグラフの話をしていきましょう。「数式」と言うと、よくこういう話が出てきますよね。「サインエックス」とか言われても何のことかわからんよな、みたいなところから話し始めていきたいと思います。

グラフを出します。x軸、y軸に色が付いているのでわかりやすいかと思いますが、サインカーブと呼ばれるグラフはこんな感じになるわけです。

これを漠然と眺めてもなかなか意味がわからんというか、「で?」という感じになると思いますが、ここで見方があるんですね。x軸は入力なんですよ。その結果が出力と考えると、ちょっと意味がわかってくるかなと思います。「y=」みたいな書き方をよくしますが、もう1つ「f(x)」という書き方もよくします。これが何なのか、区別がよくわからんという話もあるかもしれませんが、下の書き方のほうがわかりやすいと僕は思います。


というのも、下の書き方のほうが入力と出力が明らかですし、プログラムを書く時に関数を作りますよね。その形をしているので、下の形のほうがプログラムを書いたことのある人だったら理解しやすいんじゃないかなと思っています。なので、「f(x)」でグラフを書くと、こんな感じになります。


なぜこういう話を「数学、数学」と言ってやりたがるかには、理由があるんですね。例1として、突然ある入力の値の結果が欲しいことがあるんですよ。あまりないんですけどね、本当はね(笑)。たまにあるんですよ(笑)。

もっとあるのは次です。この次のスライドがけっこう大事です。xが入力だとして、入力は例えば「1」「2」「3」「4」とか、単純に増えていく値を入力に持って来やすいんですよね。その状態で変化するものを見たいということで、この関数はよく使われます。

こんな例を持って来てみました。これはよく見るプログレスバーです。これが右まで到達すると、待ち時間終わりなんだなとわかりますよね。こういう話はよくあると思います。
今は、時間と光るものの位置の関係の話をしたいのですが、例えば「sinx」じゃなくて「x2」という関数を持って来たとしましょう。そうするとこれは「0〜1」の区間でこういうカーブを描くんですね。

こういう事実を予め知ったうえで、プログレスバーをちょっと工夫してみたいと思ったとしましょう。こういうことです。同じ時間を待たせるのですが、下のほうはあとから追い上げているんですね。あまりこういうのは好きじゃない人もいるかもしれませんが、待たせる時間が最初からわかっていたら、あとから追い上げたほうがストレスは減るんじゃないのと思うかもしれないじゃないですか。実際、僕はゲームで待たせる時間をあとから追い上げる動きにわざとさせたことがあります。
それをどうやって実装するかというと、「x2」を「0〜1」の空間にしておいて、掛けるだけでこの下のプログレスバーが作れちゃうんですね。

なので、あのグラフが頭の中にある人は、簡単にこういうことができるし、「x3」にすれば、最初はゆっくりで、もっとあとから追い上げることもできるし、いろいろできます。こういうふうに入力が単純なのに出力を変化させたいという場合に、数式は非常に便利です。
では、次に、ちょっと話を変えて逆関数という話をします。今、2つ式があって、上は「x2」の式ですが、「f-1」と書いています。これが記号なんですが、逆関数の記号です。

「x2」の逆関数は何かを考える時は、1回「y」に戻しましょう。「y=x2」で、この式を「x=」で直したら、「√y」になるわけですね。厳密に言うと、xは0以上でなければいけないのですが、それはいいとして、「√」になります。すると、この「x=」に直したものを利用すれば、fの逆関数が作れます。逆関数はけっこう大事で、必ず意識したいですね。何か関数を見たら、この逆関数は何かなと思う癖をつけても損はないぐらい大事です。


では「x2」ではなくて「sinx」の逆関数は何だろうと思ったとしましょう。これは、知っているか知らないかだけの話です。

いろいろと書き方はありますが、全部同じ意味です。3つの書き方があって、どれも「アークサイン」と読むのがいいでしょう。書くとしたら一番下の書き方が普通かなと思います。「asiny」「アークサイン」ですね。これが「sin」の逆関数の単なる記号です。なので、「f(x)=sinx」、今(スライドの)右側に書いてある逆関数は、「asinx」ということになります。


逆関数を式だけで見ていると、「だから何?」みたいな話になるので、グラフでちょっと見てみましょう。まだ逆関数の話が、続いていますが、逆関数を考える時に非常に有効な考え方は、この青い点線で引いている斜め45°の線ですね。この線を中心にグラフでくるっと回します。これがどんな関数でも逆関数を作れる方法です。なので、今サインカーブが出ていますが、逆関数はこの軸でぐるっと回せばいいので、こんな感じになるわけです。図で見るとけっこう簡単な話です。

ただし、先ほども言いましたがx軸は入力なので、1つの入力で結果が2つあると困るんですね。この場合、xのある点から上に伸ばすと、2つ点がぶつかって、困るので、xに関しては「-1から1」までだし、被る部分は省くのが「asin」のグラフになるでしょう。

というわけで、これでPart1は実は終わりです。まとめとして「f(x)」という表記に慣れようという話をしました。それからグラフで大事なのは、入力と出力なんだと理解して眺めると、割とわかりやすいかなと思います。3番目、かなり大事ですが、逆関数は常に意識して生きていきたいなと思います。というわけでPart1は以上です。

続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします