 PR
PR2026.02.26
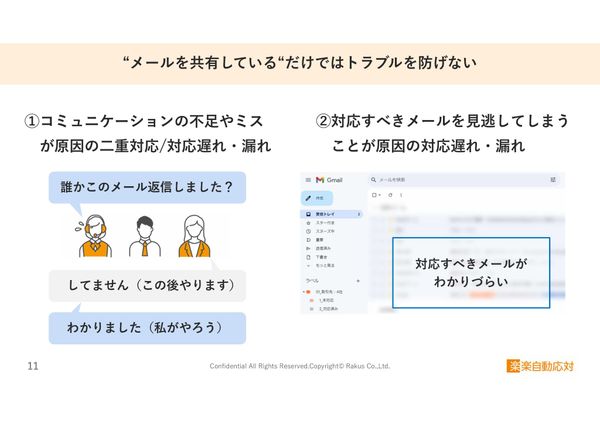
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
Optunaによる多目的最適化(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
尾崎嘉彦氏:尾崎です。今日はOptunaによる多目的最適化について紹介したいと思います。
簡単に自己紹介します。尾崎です。グリー株式会社と、産総研(産業技術総合研究所)の人工知能研究センターで研究開発職をしています。
最近の研究は、Multiobjective Tree-structured Parzen Estimator、Optunaにも入っているMOTPEという最適化手法の提案や、Optunaを使った自動結晶構造解析です。それから「CyberAgent AI Lab」の野村さん(野村将寛氏)との共著で『ハイパーパラメータ最適化に関するサーベイ』。あとOptuna関連だと『Warm Starting CMA-ES』の論文共著者でもあります。といった感じで、AutoMLとブラックボックス最適化に関する研究を普段はしています。

今日の目次です。始めに多目的最適化とはなんぞやについて、簡単に紹介します。それから、Optunaに実際に搭載されている多目的最適化手法の概要を紹介します。最後にOptunaの多目的最適化の関連機能について軽くおさらいをして、まとめに入りたいと思います。

それでは始めに、多目的最適化というものについて、多くの人はあまり親しみがないと思うので、簡単に紹介したいと思います。
いわゆるm目的最適化問題というのは、通常の1目的を最大化ないしは最小化するような最適化問題を、複数の目的に拡張したものです。同時に最適化されるm個の目的関数が存在するような問題のことを指します。
例としてここでは、成田空港からフランクフルト間の移動プランを検討するような問題を考えたいと思います。我々は、基本的に早く安く着きたいわけです。移動時間の最小化と費用の最小化という2つの目的は、通常はトレードオフの関係にあります。
例えばスカイスキャナーなどで検索をかけると、日本航空を使うと直行便で半日で着くが、ただし44万円かかる。一方で香港航空を使うと、乗り継ぎが2回で2日かかってしまうんですけども、代わりに費用は5分の1の、8万5千円ぐらいで済みます。この2つがトレードオフの関係にあって、他にも実際には航空会社がたくさんあって、選択肢がたくさんある。じゃあどれがいいんだというのが、多目的最適化の例になります。

もう少しフォーマルに書くと、右のようにこの問題は定式化されます。一般的な最適化問題だとすると、Minimize f(x) subject to xというかたちになりますが、多目的の場合にはMinimizeないしはMaximizeのf1、f2からfmまで、xは共通で、異なるfがm個あって、それらがsubject toで実行可能領域Xに入っているイメージになります。
こういうイメージは、右上水色の探索空間の各解が、左下の目的空間に写像される感じです。目的空間の点それぞれが、トレードオフを持ち得るわけですね。この例では、第2目的までしかありませんが、実際にはm次元の高次元空間をイメージすると、この中に点が散らばっているような感じになります。

多目的最適化と通常の最適化が異なる点として、多目的最適化には解の間にトレードオフが存在し得るので、基本的に唯一の最適解は、一般には存在しません。ごくまれに原点を取り得るようなアイデアルなポイントが存在する場合もありますが、基本的には一長一短の解が複数あるような状況になります。
そこで、優越関係というものを用いて解を比較します。優越関係というのは、(スライドを示し)目的空間における右上の図に表されるような関係です。この右上の図では、ベクトルA、点Aは、f1の観点でどの解よりも優れていて、ベクトルCはf2の観点でどの解よりも優れています。この時に点Bは、点Aに対してf1、f2双方の観点で劣っているので「AはBを優越する」と言います。
一方で、AとCは一長一短の関係にあるので、これらを比較不可能という意味の「インコンペアラブル」と呼びます。一般に、他の解、任意の解に優越されないすべての解の集合を「パレートセット」と呼びまして、パレートセットの目的空間での像を「パレートフロント」と呼びます。
解の優越関係は、基本的には対応する目的ベクトルの優越関係に基づいて呼ばれます。そして多目的最適化を解くというのは、基本的にはパレートセットないしはパレートフロントを獲得する、効率的に近似することになります。このパレートセット、パレートフロントを求めるのがどういう処理なのかというと、具体的な意思決定を行う前に、あり得る選択肢を洗い出すイメージです。

航空券の検索をすると、安くも早くもない結果もたくさん出てくるのですが、それらは別に要らないので、多目的最適化ではまずトレードオフの関係にある、考慮する価値のある航空券だけを先に列挙します。そしてその後意思決定を行うのが、多目的最適化の一連の流れになります。
次にOptunaに搭載されている、多目的最適化手法などについて紹介します。Optunaと多目的最適化の関わりは、多目的最適化の機械学習における応用です。多目的のハイパーパラメータ最適化やニューラルアーキテクチャサーチといった問題が近年非常に人気があります。
目的関数は、モデルの精度であるAccuracyと、あとモデルのサイズ、重さやメモリ消費量、ないしは推論の速度、モバイルデバイスにおける消費電力などが、第2目的として選ばれる傾向になります。
モデル精度がよくて消費電力の少ないモデルや、精度が高くて軽いモデルや、速いモデルなどを探索するようなタスク。これらが、Optunaが従来ターゲットとする多目的のハイパーパラメータ最適化などのタスクを素直に拡張したものなので、それらに対応できるように、Optunaのバージョン2から多目的最適化の機能が追加されました。

現在利用可能な手法は、大きく分けて2つのタイプがあります。進化型多目的最適化であるNSGA-IIと多目的ベイズ最適化であるMOTPE。ほかにも、integrationのbotorchにqEHVIというアルゴリズムがありますが、基本的には大きく分けてNSGA-IIとMOTPEが、主要なサンプラーになっています。それぞれについて簡単に紹介します。

進化型多目的最適化について紹介します。この手法は、進化計算を用いて、パレートフロントを近似する解集合を1度の実行で一気に獲得することを目的としたアプローチです。たくさんの答えを生成すると、それぞれが異なるトレードオフを持っている状況になります。
そういった個体の中で、有望なものを選んで、それに突然変異を施して、よりよい解を生成したり、あるいはトレードオフのある2つの解を交叉で組み合わせて、それらにおいて中庸な解を得ます。そうして徐々に中庸な解を増やして、全体を被覆するパレートフロントが獲得できるだろうというのが狙いです。なので進化計算としては、基本的には交叉、突然変異、次世代の選択を繰り返して、パレートフロントへの収束と、パレートフロント全体の分布を改善することを図っていきます。

そういった中で、代表的な手法がNSGA-IIという手法です。この手法では、解の優劣を非優越ランクと呼ばれる概念に基づく収束性と、混雑距離と呼ばれる概念に基づく多様性の観点から決定して、優れた解を基に次世代を生成する処理を繰り返します。

非優越ランクは何かというと、目的空間上にたくさんの点があるのですが、最も収束している解をRank1として、他の解をその収束度に応じてRank1、Rank2と層を成すように分類して、それぞれに対してランクを割り当てます。基本的には、よく収束している優越ランクが高いものを、NSGA-IIでは有望な個体とみなします。
混雑距離はどういう概念かというと、個体が密になっている場所はよく似た解がたくさんあるので、これらを間引いて次世代に残す数を調整する処理です。なので、基本的にはよく収束していた中で、広がりがうまく取れるように密な部分を間引いて残す処理になります。そしてこれらを組み合わせて、次世代を作っていきます。
実際にOptunaにおいて、NSGA-IIを使うコードを軽く紹介します。通常の最適化は、みなさんが知っていることを前提として説明するのですが、基本的にobjectiveの違いは、2目的であれば「return v0, v1」のように、objectiveが単なる値ではなくてタプルを返します。それぞれがobjectiveに対応するようなものになっているという部分と、directionsのstudyの方向性として、通常Minimize/Maximizeと書くのですが、多目的の場合には、各目的についてMinimize/Maximizeを与えるという違いがあります。
サンプラーについては、TPEsamplerの部分を、NSGAIISamplerと指定するだけで大丈夫です。実行するとこのように解いていって、ここではパレートフロントのRank1、非優越な部分、最もいい解だけが、トレードオフのある状態で赤点で表示されています。概ね、パレートフロントを近似できるような状態になっていることがわかります。


次にもう1つの多目的ベイズ最適化について説明します。多目的ベイズ最適化は、目的関数や探索空間についてベイズ的なモデルを構築して、獲得関数と呼ばれる基準を用いて有望な解を効率的にサンプルする手法です。これは原理的に、進化計算とは大きく異なるアプローチです。
モデルの対象は大きく分けて2つあって、目的空間を近似するようなモデルを作るのが、ほとんどの多目的ベイズ最適化手法が採るアプローチです。もう1つとして、探索空間の有望領域などをモデル化する方針があって、MOTPEはこの後者のモデルになります。

MOTPEは、Optunaの標準の多目的最適化におけるアルゴリズムであるTPEと呼ばれる手法を多目的最適化に拡張したもので、2020年にできた新しい手法です。モデルは、基本的には探索空間内の有望・非有望な解について、カーネル密度推定を行うことで決定されます。
この有望と非有望をどうやって決めるのかというと、目的空間における先ほどの非優越ランクなどを用いて、非優越ランクが1、2の解はよくて、大きなものは悪い。具体的にはある程度の個数の閾値を設けて、そこで2つに分けます。
そして、それぞれの目的空間のベクトルに対応する解の集合について、密度推定を行って、探索空間でよい解のグループと悪いグループの密度が、それぞれ個別に推定されます。

MOTPEは、モデルを構築した後は、Expected Hypervolume Improvementと呼ばれる獲得関数によって、評価する解を決定していきます。
ここでHypervolumeについて紹介します。Hypervolumeは左下の図にあるグレーの領域のことです。目的空間にものすごく悪い点、例えばf1、f2両方ともメチャクチャ悪い値を取っている点rを考えて、こいつを参照点と呼びます。そしてその参照点rと、例えばここでは集合Yとして3点可視化されていますが、私たちが見つけた目的ベクトルたちによって囲まれる領域の体積をHypervolumeと呼びます。

このrは任意ですが、基本的には非常に悪い点を取る点を勝手に置きます。そうすると、このグレーの部分が、大きさを測れて、何らかの値を持ちます。パレートフロントをとる時に、このrとそのパレートフロントによって成される領域の超体積は、最大化されることが知られているので、Hypervolumeを最大化することが、パレートフロントを獲得することになります。
基本的にMOTPEは、このHypervolumeを増加するように点を選んでいきます。EHVIというのは、今すでにある集合Y*に新しい点y=f(x)を加えた時に、Hypervolumeが増加する量の期待値に対応するので、これを最大化するxを選ぶと、期待値で最もHypervolumeを新たに点を加えた時に増加させられる解になっています。
実際には、有望・非有望領域の確率密度をl(x)、g(x)とした時に、数学的にargmaxのEHVIが、この密度比を最大化する点として得られることがわかっているので、そういった点をMOTPEでは採択します。
Optunaにおいて、MOTPEを使うのは非常に簡単で、先ほどのNSGAIISamplerをMOTPESamplerに変更するだけです。実行すると、こんなふうにベストトライアルな赤の部分、パレートフロントの近似が効率的に得られます。


これらの2つの手法を比較してみます。青点がNSGA-II、赤点がMOTPEですが、初期化時点でほぼパレートフロント近くの点が取れてしまう簡単な問題の場合は、がんばってパレートフロントに向かって収束する必要性があまり高くないので、どちらを使ってもだいたい解けてしまいます。

次に、ランダムに生成したぐらいではパレートフロントから離れた点しか取れないような、難しめの問題で実行してみます。ベイズ最適化はやはりモデルを使うので、効率性は高くて、収束はMOTPEのほうが速さは際立っています。NSGA-IIは、よく見ると右上から左下に線が伸びるように解が生成されて、少しずつ収束していっている様子は見られるんですが、MOTPEには追いついていないです。

やはり評価回数が限定されるようなAutoMLみたいな問題には、MOTPEは適した性能を持っていると言えます。
一方で、予算(評価回数)がたくさんある場合、過去の解をすべて考慮してしまうMOTPEだと、実行時間は評価回数に対して非線形に伸びてしまいます。他方NSGA-IIは進化計算で、毎世代固定サイズの個体群しか考慮しないので、評価回数に対して実行時間は線形にしか伸びていきません。
また、経験的にですが、MOTPEのだいたい適した評価回数は、多くても1,000回程度までで、この例だと1,000回で15分か20分ぐらいです。他の多目的ベイズ最適化と比べるとずっと速いのですが、NSGA-IIに比べるとやはりお話になりません。

個人的には、実務では序盤はMOTPEで、遅くなってきたらNSGA-IIに切り替えるのもありかなと思います。それから純粋な多目的の離散最適化だと、NSGA-IIがよいことが経験的にわかっています。MOTPEは離散も扱えるのですが、やはり0-1整数系化学などは、遺伝子を0/1で直接コーディングできる、遺伝的アルゴリズムのほうが適していると思います。


最後に、Optunaの多目的最適化関連機能について軽く紹介します。得られた解の可視化には、2次元や3次元であれば散布図が便利です。Optunaですでに提供されていて、plot_pareto_frontなんちゃらみたいなものに対して、studyを渡してあげると、plotlyベースや、matplotlibベースの可視化ができます。
4次元以上の場合は、パラレルコーディネートを使って、f1、f2、f3、f4などを線でつないで可視化する方法がけっこうよく行われますが、こちらはまだOptuna自体には入っていないので、自前で準備が必要です。

もう1つが評価です。評価はいくつかの指標がありますが、多目的最適化の結果の良し悪しを数値として評価する方法の例として、少し前に紹介したHypervolumeを使う手があります。
Hypervolumeの計算関数は、今のところは開発者向けのAPIなのですが、すでにOptunaの機能として利用が可能です。ステップごとに得られたベクトルを持ってきて、Hypervolumeを計算して、それらを最終的にグラフとして可視化しています。
これらは、獲得した解によって達成されるHypervolume量の変遷をプロットしたもので、単目的でいうoptimization historyグラフのベストバリューに相当する役割です。評価回数を経るごとに、Hypervolumeが増えていって、やがてはサチっていく様子が見て取れます。

こういった手法を使うことで、客観的に多目的最適化の良し悪しを評価できるでしょう。
まとめに入ります。多目的最適化というのは、パレート最適解の集合を獲得することが目標です。得られたパレート最適解を基に、意思決定を下すことで、実務等に役立てられます。

Optunaは、進化型多目的最適化と多目的ベイズ最適化の2タイプの手法を提供していて、前者は汎用的で、NSGA-IIはその最も代表的な手法です。一方で後者は、AutoMLに特化した手法で、MOTPEはハイパーパラメータ最適化手法TPEの多目的版に当たります。今回は、Optunaの多目的最適化関連機能も紹介しました。
多目的最適化ですが、やはり単目的な最適化に比べると活用事例も開発者も少ないので、今回をきっかけに、ユーザーや開発者が増えるとうれしいと思っています。ご清聴ありがとうございました。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします