 PR
PR2026.02.26
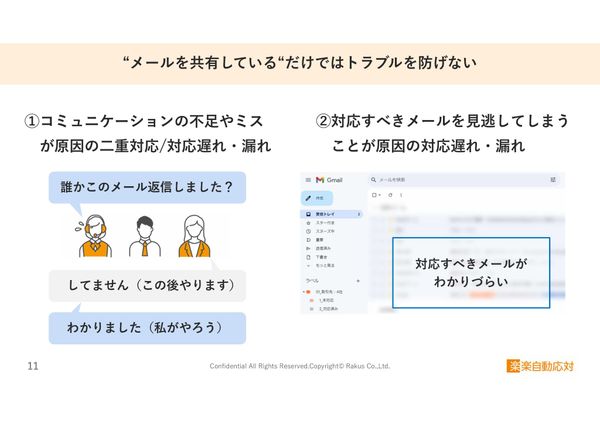
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
gloss: 動かして遊んで学ぶHaskell(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
lotz氏:「gloss: 動かして遊んで学ぶHaskell」というタイトルで発表させていただきます。
まず自己紹介すると、lotzといいます。
僕もHaskellは趣味で、ふだんは半蔵門で働くエンジニアです。SNSのIDをスライドに載せているので、質問があればTwitterで、気軽に声かけてください。
さっそくですが、Haskell入門したあとにありがちなパターンとして「なにか作りたいけどネタがない」があると思います。
さっきCLIツールの作り方(の発表)がありましたが、それも1つの手だと思いますが、今回はもっと想像力を刺激するような実装例を紹介したいと思ってます。それが、このglossというライブラリです。
glossは、2Dグラフィックを簡単に描画できるライブラリです。
アニメーションとかシミュレーション、マウス・キーボードのイベント処理にも対応してるので、ゲームとかも作れます。目に見えるものがすぐに作れて楽しいライブラリです。
今回の発表の裏目標は、Twitterとかで「glossで作ってみた」みたいな報告がたくさんされるとうれしいなというところです。みなさん、よろしくお願いします。
まず、Hello Worldです。
glossで書くと(スライドを指して)こんな感じでメイン関数があるんですけど、displayというやつが、glossが提供している関数です。
表示しているHello Worldは、message = text ”Hallo World”で作ってます。コードはあとで詳しく説明していきますが、とりあえずこれを単純に実行すると「Hello World」と表示されます。……今は残念ながら画面の外に「World」がはみ出てしまって「Hello」しか見えませんが(笑)。
(会場笑)
こっちのDisplayという関数は3つ引数を取ります。
1つは描画モード。ウインドウで表示するか、フルスクリーンで表示するかを選択できます。次に、背景色。さっきはwhiteで、白い背景になってたんですけど、色を選べます。最後に、描画する図形。この3つを入れると、ウインドウが立ち上がってその図形をパッと表示してくれるという、非常に簡単なライブラリです。
displayのほかにも3つ、大事な関数があります。
1つはanimate。時間変化を伴う図形ですね。displayの、さっきPictureだけ渡してたところが、経過時間を受け取ってPictureを返す関数になって、まぁあとは感覚でなにやるかわかると思うんですけど。
(会場笑)
こういうふうに、アニメーションが簡単に作れます。
あとはsimulateという、抽象的なモデルの時間発展とそのモデルを絵にする関数を与えるとシミュレーションしてくれる関数。最後に、イベントハンドラを渡すとキーボードとかマウスの処理ができるplay。基本的な関数はこういったところです。
次に「どういう図形を描けるのか」を説明していきます。
まず基本的なものが、線分です。
Lineという関数を使うと、線分のPictureを作ることができます。これ、引数はFloatとFloatのタプルのリストなんですけど、左のFloatがX座標、右のFloatがY座標で、そのタプルのリストなので、点列を表してるわけです。この点列にピーッと線を引いてくれるというものがlineです。
次にcircleです。
半径を渡すと、その半径の円を描いてくれます。circleとcircleSolidの違いは、中が塗りつぶされてるか塗りつぶされてないかです。
次に、長方形。Rectangleは、
幅と高さを与えるとその幅と高さの長方形を描いてくれる関数です。circleと同じように、塗りつぶされてる・塗りつぶされてないという違いで2種類あります。
text。
最初のHello Worldで使ったやつですね。Stringを与えるとそのStringのPictureを作ってくれる関数で、うまくやれば「Haskell Day 2018」とか、文字を描画することができます。ただ、フォントの指定とか日本語の表示ができないという欠点はあります。
次、Pictureの変形について話していきます。
まず、今までPictureを作る関数をいろいろ見ましたけど、あのまま単純にPictureを作ると、原点のところにボンと表示されてしまうんです。画面上の任意のところに表示するためには、作ったあとに移動させてやらないといけません。
そこで出てくるのがtranslateという関数です。
X座標の移動量・Y座標の移動量を入れると、PictureをPictureに変形する関数になります。
glossの座標系は、こんな感じで画面の中心が原点になってて、右にいくとX座標が増える、上にいくとY座標が増えるという座標系です。
scaleが拡大・縮小させる関数で、X座標の拡大量・Y座標の拡大量を入れると、PictureをPictureに変形させる関数になります。(スライドを指して)これは、さっきのanimateっていうglossの関数を使ってアニメーションで表示してます。こんな感じで図形を拡大・縮小することができます。
これらを使って、Hello Worldをちゃんとやってみましょうという話です。
最初のスライドと変わったところはmessage = translate (-160) 0 , scale 0.5 0.5ですね。textで作ったHello Worldを、これはふつうの関数合成なので、まずscaleで半分の大きさにしてからtranslate、X座標をマイナス160で左にぐいっと持ってくると……ちゃんと真ん中に、Hello Worldと表示されました。
別のPictureの変形としては、rotateというやつがあって、時計回りにPictureを回転させる関数です。
(スライドを指して)この例はanimateでアニメーションさせてます。
次はcolor、これは図形の色を変えることができます。colorでPictureを変形すると、black、white、red、green、blueみたいな値がデフォルトであって、rgbaを指定して自分の好きな色に変形することもできます。(スライドを指して)こういう赤い四角とか青い四角とかを描けます。
最後。実は、aiyaさんの発表でもあったんですけど、Pictureはモノイドのインスタンスになってます。
Pictureのモノイドってなにかというと、図形の合成というか、レイヤーの合成みたいな感じです。
今までは、Pictureを1個ポンと作る関数とそれを変形する関数しかなかったんですけど、じゃあ「丸と四角を同時に画面上に描きたい時どうするんだ」ということです。
それぞれ別々にPictureを作って、モノイドの演算で合成すると、丸と四角を同時に描いた1つのPictureみたいになって、無事1つのPictureにすることができます。これが、Pictureのモノイド演算です。
ちなみにモノイドなので単位元もあるんですが、単位元はブランクという、まったくなにもないような図形になってます。
さっそくこのglossを使って、いろいろエグザンプルを紹介したいと思います。まず、物理シミュレーション。
Haskellで二重振り子のシミュレーションを書いた。実はこの振り子50本あって初期値を1兆分の1ぐらいずらしてあるので途中からめちゃくちゃ分岐する pic.twitter.com/3dh4Metcpj
— lotz△ (@lotz84_) 2017年5月22日
これは僕の1年前のツイートで「二重振り子で実験をした」ってやつです。今日はこの二重振り子を、glossを使って作っていきます。
二重振り子のシミュレーションにはsimulateという関数を使います。
simulateの引数はディスプレイモードと背景色と、1秒あたりのステップ数。この3つと、さらに3つあって、あとの3つが重要です。
まずmodelは、型変数です。modelという型があるわけじゃなくて、ここで自分の好きなmodelを入れることができます。それから、modelと、それをPictureに変形する関数。最後の「(ViewPort => Float => model => model)」というのは、ViewPortはいいとして、経過時間を入れてmodelを変化させる関数ですね。
イメージとしては、スライドに図示したような感じです。Simulateはアニメーションをやるんですが、裏で実はmodelの時間発展をシミュレーションしている。イメージとしては、抽象的なmodelがあって、そのmodelから図形への変換関数があります。modelにはまた別に経過時間を受け取って発展していく関数があって、それが随時図形に変換されて、glossを通して我々に見えているということです。
こういう考え方で、シミュレーションを作っていきます。
じゃあ二重振り子におけるmodelはなにかというと(スライドを指して)こういう、物理とかで出てきたようなやつですね。
二重振り子は、重りが2つあって、そのX座標・Y座標なわけですけど、角度を2つ指定すれば二重振り子の位置はピタッと決まるわけです。だからmodelは、この角度2つですね。
あとは、時間発展。二重振り子(を作るに)はこの運動方程式を解けばいいんですけど、解くのがすごく大変(笑)。なので、hamiltonというライブラリを使います。
hamiltonは「ハミルトン力学と自動微分を利用して一般化座標系における物理をシミュレーションしてくれるライブラリ」です。……これ、直訳で、完全には理解してないんですが(笑)。
まぁ、便利なライブラリで、hamiltonの中にstepHamという関数があります。これは、経過時間とSystemという物理系を入れると、PhaseをPhaseに変換してくれます。だからPhaseを抽象的なmodelにすれば、glossでそのまま当てはめて使うことができるという便利なやつなんですね。
今、作らなきゃいけないやつがこのSystemなんですけど、これはなにかというと、2つの型引数を取る型です。1つ目の引数は、デカルト座標の次元。もう1つの引数は一般化座標、便利な座標の次元です。とりあえず2つ座標系を考えるんだな、ということだけ覚えておいてください。
このSystemの値を作るために、mkSystemという関数を使います。mkSystemに必要なものは3つです。1つ目は質量、重さ。慣性です、正確にいうと。あとは、2つ存在する座標系の座標変換の関数。最後に、座標系における位置エネルギー。この3つを与えると、Systemを作ることができます。
なので、二重振り子で考えると、あとで見るんですけど、すごく簡単に作れるので便利です。
最後に、今回modelとして採用するPhaseは、スライドには一般化座標と一般化運動量って書いてあるんですけど、まぁ位置と速度みたいなものです。そういう基本的なパラメータが入ったやつです。
ではさっそく、二重振り子におけるSystemを作っていきましょう。
(コードの長さは)これだけで作れます。Systemを作るには質量と座標変換と位置エネルギーが必要ですが、今回はちょっと簡単にするために、棒の長さも質量も重力も全部1としておきます。
まず、座標変換。スライドで、2つ座標があるのは、この二重振り子の重り、2つあるので、まずはそれぞれの平面上のX・Y座標の軸。これで2次元×2で、4つあるわけですね。この「System 4」が、4次元のデカルト座標です。
次、この「2」は、この振り子を表すための別の座標として、この角度2つをとることができるので、この2次元として「2」です。
今、その角度の座標系と、デカルト座標系。空間中の座標系の2つがあったと思うんですが、座標変換としては、角度の座標系から空間中への変換を考えます。
これは単純な3角形で、三角関数を組み合わせれば単純に書けるので、あんまり詳しくは説明しません。位置エネルギーは、高さを入れてやればいいでしょう。重力も1なので。
次、二重振り子を描画していきます。
モデルからPictureへの変換の関数ですが(スライドを指して)こういう絵を描きたいわけです。この絵はどういうもので構成されてるかというと、棒と、重りで構成された振り子が2つあるんですね。それを愚直に作っていきましょう。
rectangleSolidで幅1の棒、circleSolidで中の詰まった円を作ります。それをstickとweightというふうに置いて、このstickとweightをモノイドで結合してやる。これを適切に回転させたやつが、pendulum1。もう1つがpendulum2。この振り子2つをモノイドで合成してやれば絵が描ける、という単純な話です。
必要なものが揃ったので、simulateに入れてやりましょう。
simulateの時間発展は、hamiltonのライブラリが提供している関数をほとんどそのまま入れてやればできます。これで、無事、二重振り子のシミュレーションを作ることができました。
フルのコードをgistに載せているので、あとで見ていただきたいと思います。(スライドでは)非常に簡潔に書いてあります。
あとは、これを初期値をずらして50本用意すれば、冒頭の動画は簡単に作れます。あと、Systemの型変数でmとnがありましたが、あそこの値を変えれば簡単にn重振り子とかも作れるし、がんばればmとnを型変数にしたまま、最後にタイプアプリケーションとかで「6」とかって指定して、6重振り子を作るというようなアプリケーションも作れます。ぜひ試してみてください。
次に「コモナドで作るライフゲーム」にいきます。
コモナドってなにかというと、そんなに馴染みがないかもしれないですが、単なる型クラスです。コモナドの説明には、モナドっていうよく知ってるやつを先に持ってきたほうがいいと思ったので、まずモナドを見ます。
モナドには、pureとjoinっていう2つのメソッドがあります。モナドのpureは、値をとってモナドに包む関数ですけど、コモナドにもそれに対応するものがあって、extractってやつです。extractは、包まれているデータ構造から値を1個取り出すというものです。
モナドのjoinは、二重に包まれたやつを一重に包まれたやつに潰すというメソッドですけど、コモナドは逆で、一重に包まれたやつを二重に包む。モナドの感覚だと「単純に包めばいいじゃん」ってなると思うんですが(笑)。コモナドにはreturnとかpureみたいなものがないので、こういうメソッドが別に用意されてます。
コモナドにまつわる話、やっぱりいろいろあります。
「コモナドはモナドの圏論的双対」ですとか、有名なモナドに対応するコモナドがあるんですね。Reader、Writer、StateにはEnv、Traced、Storeみたいに対応してたり、みんな大好きZipperもコモナドのインスタンスだったりします。Lensっていうやつは、余状態余モナドの余代数、みたいな……(笑)。
(会場笑)
つまり、Storeコモナドの余代数。で、コモナドを使えば実は画像のフィルタ処理とか実装できたり。いろいろおもしろいやつなんですけど、今日は詳しい話は割愛します。
今日作りたいのはこのライフゲームというもので「生命の誕生・進化・淘汰のプロセスを再現した簡易的なモデル」っていう仰々しいやつなんですけど、非常に見てて楽しいゲームですね。
平面上に、生存状態と死亡状態という2つの状態を持ったセルをマス目上にバーッと敷き詰めて、決められたルールで時間発展させていって、その様子を眺めるというゲームです。
時間発展には4つのルールがあります。
まず、死亡状態のセルから生存状態のセルに変わるルールとして、その死亡セルの周りに生存セルがちょうど3つあれば、次のステップで生存になります。生存セルが次のステップでも生存し続ける条件は、隣接する生存セルが2つか3つ、どっちかならば次のステップでも生存セルのまま生き残るというものです。
生存セルが死亡セルに変化するルールは2つあって、過疎と過密です。生存セルの周りに隣接する生存セルが1つ以下なら次のステップで死亡セルになります。逆に多すぎる、4つ以上の場合にも死亡セルになってしまいます。ちなみに「隣接」は、(斜めも含めた)8つのマスで考えてます。
このルールで時間発展させると、いろいろおもしろいパターンが出てくるんですけど。ライフゲームって、すごく死にやすいんですよ。平面の上に点が1個だけポンと置いてあると、次のステップでは過疎で死んでしまいます。
一瞬で死んじゃうんですが、このブロックって実は4マスぶんあって、(スライドを指して)左上のやつは1個の周りに3つあるので、次のステップでも左上のやつは生存し続けます。それが右上も右下も左下も、お互いにお互いの3つで生存し続けるので、ずっとこのまま固まってるという「ブロック」という図形です。
「ブリンカー」は、縦棒の上と下が過疎で消えて、でも横のところはちょうど周りに3つあるから次のステップで生存するというパターンを繰り返して、周期2を持つ図形です。
もっといろんな周期を持つ図形もあります。おもしろいのが「グライダー」で、これは周期を持たないけど、ずっと平行移動し続ける。スライドではgifだからパッと元に戻るんですけど、なにもしなければずっと右下に無限に移動し続けます。
そういう図形が出てきたりと、見てるだけでおもしろいゲームです。
これを作っていきましょう。まず、ライフゲームを作るために、Zっていうデータ構造を使います。
イメージとしては無限に広がるリストがあると思ってもらって、そのリストの1つの要素に注目したやつが、このZです。このZのリストと要素リストをとります。
真ん中が、注目した要素。左が、その注目したやつよりも左にずーっとある無限リスト。右が、注目した要素よりも右にある無限リストだと思ってください。そういうデータ構造です。
これに対して、leftとrightという操作を考えます。イメージが掴めればわかると思うんですが、注目してる点を1個左にずらすものがleftで、1個右にずらすものがrightという関数です。
さっそく、このZをコモナドのインスタンスにしていきましょう。
まず、extractというものがあったと思います。extractはZから1個要素を取り出す関数です。Zは、無限リストの1つの要素に注目したようなデータ構造なので、取り出す要素っていうのは自明ですね。それを素直に取り出しましょう、というものがこのextract。
おもしろいのが、duplicateのほうで、型としてはこの「Z a」を「Z(Z a)」に変換するんですけど(スライドを指して)イメージはこんな感じです(笑)。これ、口で説明すると大変なんですけど。
「Z a」が無限リストだったわけですね。さらにその要素がまた「Z a」になっていて、その要素1個1個が無限リストになっている。2次元的な構造を考えてもらうと、わかりやすいと思います。
実は、中に入っている注目してる点が、1個ずつずれていくように作っているわけですね。だから、この「Z a」をduplicateします。すると「Z(Z a)」になるわけですが、外側のZは奥行き方向の無限リストを表していて、注目してる「Z a」というものが1個ある。内側の「Z a」は、1個1個の横に並んだ無限リストを表しています。
(スライドを指して)上から見た図です。それぞれ全部、注目される点を持ってて、上から見ると、その点が1個ずつずれていくというイメージです。こういうふうにduplicateを作ってます。
Zについて、力を入れて説明したんですけど、実はZは1次元なので、ライフゲームの作成には向いてません。なので、平面の同じような構造を、Zを使って作っていきたいと思います。
それがこのZ2というやつです。中身はさっきの「Z(Z a)」という、Zを2回やって、無限リスト×無限リストで無限平面、みたいなものを作ったやつです。これをすぐコモナドのインスタンスにするんですけど、注目している「Z a」に注目してる1点があるから、Z2というデータ構造が与えられると、注目している1点は自明に定まるので、それをとりあえずextractすればよいということです。
今度はduplicateです。今考えているZ2は、無限平面の中の1点に注目したデータ構造なんですね。それをduplicateするとどうなるかというと、注目されてる点を1個ずつ平面上にずらしたZ2が、無限個平面上に並んでるということです。平面が無限個平面上に並んでいる、2回「平面」といってるところが、このZ2、「Z a」という、2重になってる型の気持ちを表してると思ってください。
いよいよ準備ができたので、ライフゲームを作りましょう。Z2 Boolというものを考えます。ライフゲームのセルの状態は2個なので、Trueに生存セル、Falseに死亡セルを割り当てます。
まず、Z2 Boolが与えられると、Z2は無限平面の中の1点に注目したデータ構造なので、1点という考え方ができるわけですね。
このneighboursという関数は、その注目してる1点の周りにある生存セルの個数を考える関数です。ちょっとカッコよく、パターンマッチで近傍のデータを取ってきて、この中の生存セルの個数を考えます。
次、lifeという関数。これがライフゲームの時間発展のキモになる関数です。
Z2 Boolが与えられると、注目してる1点があるわけです。その1点が次のステップで生存するか死亡するかを判定するのが、lifeです。実装は簡単で、周りの生存セルの数を数えて、あとはライフゲームの時間発展のルールに当てはめればよいと。lifeのイメージは(スライドを指して)こんな感じですね。1点に注目した無限平面から、その1点の次の状態を返します。
最後に、コモナドが力を発揮します。lifeっていう、Z2に包まれたやつを、Bool1個に返す関数。平面の中の1点から1点への関数を、コモナドのextendに入れると、ライフゲームの実装が完了します。
これ、どうなってるかというと、lifeにextendを適用した関数がここのイメージです。extendはコモナドの抽象的なメソッドで、まずduplicateしたあとに第1引数の関数をfmapするという関数です。これは、コモナドという抽象的なレイヤーで、そういう実装になっています。
それを今回のZ2で考えると、Z2のduplicateって、注目してる1点を平面上にずらしたやつを無限平面上に並べるものでしたよね。その平面上に並んでいる1個1個の平面にlifeを適用すると、平面の上に並んでた平面が全部1点に潰れて、平面が1個できるわけです。それが、1ステップ時間発展したライフゲームに対応しているということです。
これでライフゲームの実装は終わりです。最後はちょっと魔法のような感じで(笑)。描画に関しては、いっぱいあるんですが、TrueとFalseで白黒の四角を変えて並べれば終わりなので、あとで(スライドを)見てください。
これで最後、simulateっていう関数に入れます。この時間発展のところに、まさにextend lifeという名前のやつがそのままぶち込まれています。これで、ライフゲームの時間発展が、コモナドを使って簡単に書けます。無事、グライダーを作ることができました。
ライフゲーム、作ったんですけど……さっきから言ってるように、Z2ってデータ構造的には無限平面なんですよね。でもなんでこれが動いてるかというと、描画する領域が限られているから。有限項評価すればこの描画には十分なので、遅延評価の恩恵を受けて描画できてる。
でも描画領域のセルに影響を与えるセルは、時間が経つに連れてどんどん増えていくわけです。どんどん計算量が増えるので、実はこのグライダー、ゆっくり減速してるんですね(笑)。
(会場笑)
考えてるけどまだやってないこととしては、さっきのZ2を平面じゃなくてトーラス上に実装するようにして、コモナドのインスタンスにすれば、うまく有限の領域内のライフゲームを作れるんじゃないかなと。まだ取り組めてないので、興味がある人はぜひやってみてください。
最後。「glossの中でIOを使いたい」というモチベーションがあるかと思います。例えばゲーム作りたいとか、シミュレーションをやりたいと思ったら、やっぱり乱数を振りたいですし、ネットワーク通信とかセーブデータのファイル出力とかしたい。あと、FRPライブラリと組み合わせてオレオレアーキテクチャ作りたいとか。
glossのパッケージを眺めてみると、InterfaceIOという、それっぽいやつがあります。この中、いろいろあるんですけど、simulateIOとplayIOというやつがあって、こいつらを使えば、副作用を起こすことができます。
最初のピュアなやつと、比較用とで比べてみます。
ちょうどsimulateは描画する関数と、あと時間発展の関数で副作用が起こせるようになってます。それで、playはイベントハンドラの関数で副作用が起こせると。
これを使って、カオスゲームという例を紹介します。
どういうゲームかというと、平面上で多角形を1個決めて、また別の点を1個取って、多角形の適当な頂点と、適当な点の内分点を取ります。その点を新しい点として、また多角形の適当な頂点とその内分点を取る、ということをランダムで繰り返すと、フラクタルな図形ができるというものです。
例えば、多角形として三角形を考えますね。
三角形を取って、適当な点から、1/2してると思うんですけど、内分点を計算します。このとき、uniformRという、乱数を振る関数で0、1、2の適当な頂点を取ってきて、その適当な頂点との内分点を計算します。
イベントハンドラとしては、今回、適当な点をマウスでクリックして決めようと思うので、マウスクリックをハンドリングします。
マウスクリックは、EventKeyの、MouseButtonの、LeftButtonが、DownされたところのX・Y座標をmodelのリストに加えるという感じです。modelとしては点列を考えてるので、その初期値をポンと与える、みたいなイメージです。描画は、点に沿ってひたすら丸を打っていけばいいので、すごくシンプルです。
それで作ったものがこんな感じです。
まず右上のところに点を打って、そのあと適当な点との中点を無限回取り続けていくわけです。すごくランダムなアルゴリズムのように見えるんですけど、こういうフラクタル的な、きれいな図形ができていくという、おもしろいゲームです。
これ、四角形だったり五角形だったり、ほかのいろんな多角形でもこういうフラクタル図形ができます。その場合は内分点じゃなくて、別の比率で取ったりしますが。
まとめです。
glossを使えば、簡単に2Dグラフィックを扱えます。hamiltonを使えば、運動方程式も簡単に扱える。コモナドを使えばライフゲームが作れる。glossはIOも扱えます、ということです。
次はみなさんも、glossで遊んでみてください。ご清聴ありがとうございました。
(会場拍手)
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします