 PR
PR2026.01.19
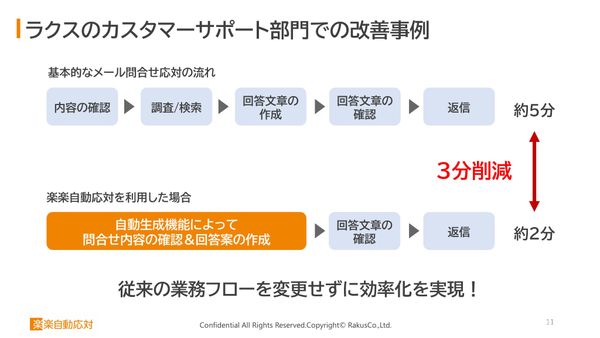
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
コピーリンクをコピー
ブックマーク記事をブックマーク
『片付けパパの最強メソッド』の著者・大村信夫氏が旬なトピックでゲストと対談するシリーズ。第9回目は『「数学的」話し方トレーニング』の著者で、ビジネス数学教育家の深沢真太郎氏が登壇。「『伝える』から『伝わる』コミュニケーション術」をテーマに、数学的な5つの動作や、物事を細かく分けることの重要性について語られました。
深沢真太郎氏(以下、深沢):「数学的思考」は、説明という行為ととても仲良しです。だから今日、私が「説明する」という文脈でお話しができるんです。じゃあ具体的なところにいきますね。説明がうまい人がやっている数学的な、さっき「動作」と言いましたよね。実はここに書かれている5つです。

大村信夫氏(以下、大村):へぇー……「定義」「分解」「比較」「構造化」「モデル化」。急に難しく感じてしまうんですけど。
(会場笑)
深沢:「出た、なんだか数学っぽいのがきたぞ」という感じですよね。
大村:共感でいいんですよね? 僕が「バカじゃない?」という話ではなくて。
深沢:今、会場のみなさんもこうやって「うんうん」と頷いているので。そうそう、「数学~」とか「ロジカル~」みたいな先生はこういう言葉を使うわけです。やな感じです。
大村:使いますよね、そうそう(笑)。
深沢:でもぜんぜんいやな感じではないですよ。
大村:ではないんですか?
深沢:ではないです。なぜこの5つが数学をする時にする行為かは、みなさまにも納得していただきたいので、少し説明に付き合っていただきたいと思います。本当に簡単な話です。
大村:1番目が「定義」でしたよね。
深沢:はい、「定義」。定義とは、「~とは~である」と言葉にすることです。例えば、何だろうな、「人生」を定義してください。
大村:それ、難しくないですか?
深沢:(笑)。
大村:いきなり超難題というか、解けない人のほうが多いんじゃないですか。
深沢:そうですか? じゃあ大村さん、「休日」を定義してください。
大村:休日?
深沢:大村さんにとっては、「休日とは~である」。
大村:みなさんもよかったら「休日とは」で、チャットに書いてください。
深沢:そうですね。そうか、そういうふうにチャットを使えばいいですね。「休日」の定義をお願いします。人によってぜんぜん違うよね。
大村:「仕事をしない日」って。
深沢:そうそう、そうですね。
大村:僕もこれを言おうかなと思っていました。
深沢:「休日とは仕事をしない日である」。
大村:「義務がない日」。
深沢:「義務がない日である」。
大村:でも「仕事をしない日」が多い。「意義がない日」とか、「安息日」「旅行する時」。なるほど。「自分のために時間を使える日」。こう見ると、ある程度類型化はできるものの、みなさん違いますよね。
深沢:はい。言葉は少し違ってきますよね、
大村:「旅行してもよい日」なんていう。
深沢:「休日とは、寝坊をしてもよい日である」。
大村:いいですね。
深沢:すばらしい定義じゃないですか。
大村:なるほど。
深沢:そこまではOKですよね。数学では、この行為を最初にするんですよ。例えば、書いてありますけども、「素数」というものがありましたね。
大村:素数ってあれでしょう?
深沢:あれですよ。
大村:1とその数でしか割れない数。自然数。
深沢:おお、すごいすごい。そう。1と自分自身以外では割り切ることができない。だから2とか3とか5とかは、「素数」なんて言いますね。それが「素数の定義」です。
大村:なるほどね。
深沢:ということは、「素数」について勉強したい、研究したい時は、まず最初に「素数とはこういう数である」と定義しないと始められないと思うんですよ。だから円の勉強をしたかったら、「円とはこういう図形である」と定義しないと始められないんですよね。
大村:なるほどね。
深沢:つまり何が言いたいかというと、数学という学問は、「定義をしないと始められない」という作法があるんです。
大村:なるほど。
深沢:ここまでどうですか。
大村:ちょっと、わかってきました。さっきの数学と思考とかが仲良しだから、説明の前にくる思考は、この「定義」という要素が重要ではないか、みたいな感じでしょう。
深沢:お、鋭い。その通りです。あとでちょっと出てきますけどね。
大村:なるほど。
深沢:そういうことです。オンラインでご参加のみなさんも、「定義をしないと始められない」という作法があることだけ、覚えておいてください。
深沢:2番目、「分解」。これは、優秀なみなさんはよくご存じですよね。「物事を分けましょう」なんてよく言いますよね。
大村:はいはい。
深沢:(ルネ・)デカルトさんという哲学者も、「難しい問題は小さく分けて考えるのがいいよ」と言いますね。その通りだなと思います。そして、なぜこれが数学と仲良しかというと、さっき大村さんが、「微分・積分」とおっしゃっていましたね。
大村:微分・積分。
深沢:「因数分解」なんて、言葉としてよく聞きます。
大村:でも僕ね、微分・積分って、高校で習ってから一度も使っていないですよ。
深沢:実は数学の考え方はいろんなところで使われているんですよ。ここで注目してほしいのは、「因数分解」にしろ「微分・積分」にしろ、使われている言葉があることです。
大村:「分ける」という漢字がありますね。今気づいた。
深沢:その通りですよ。「分ける」という言葉が使われている。つまり数学とは、物事を細かく小さく分けていくことで、「わからなかったものがわかるようになるよ」とか、「解けなかった問題が解けるんだよ」と教えてくれる学問だということです。
大村:なるほどね。
深沢:だから「分解」という動作は、とても数学的ということですね。
大村:「おお」と、チャットできているな。こういう反応はすごくいいですね。ナイスリアクションです。
深沢:ナイスリアクション。もっとちょうだい。
深沢:では3番目。「比較」。これはわかりやすいですよね。比較なくして数学は絶対にできないです。
大村:イコールって比較ですか?
深沢:そうですね。「こっちとこっちを比べて同じです」という意味なので、比較です。
大村:ああ、そうなんだ。
深沢:「こっちのほうが大きいですよ」。
大村:不等号とか。
深沢:そう、よくご存じで。だから数学とは、比較をすることで行う営みです。だから、比較も実は数学的な行為だということです。
4番目「構造化」。少しだけ抽象度が増すので、ここはちょっと丁寧にいきたいと思いますが、言葉が嫌ですね。
大村:そうですね。
深沢:(アンリ・)ポアンカレという数学者さんが、「数学とは異なるものを同じものとみなす道具です」という言葉を残しているんですね。
大村:僕だけじゃなくて、みんなポカーンです。
深沢:大丈夫。ここからわかるから。でも、意味がわからないでしょ?
大村:意味がわからないですね。
深沢:例えばスライドのこれは、ポアンカレの言葉で、下に2つ数式があるのが見えますか? ちょっと読んでみてください。

大村:「100X+100Y=100」。
深沢:はい。もう1個も読んでみてください。
大村:「X+Y=1」。
深沢:そうですね。この2つの数式って表面上は違う式ですよね。
大村:表面上はね。
深沢:違うものですよね。でも数学をちょっとお勉強したみなさんだったら、この2つが同じ式であるともわかるはずです。
大村:わかりますね。
深沢:そうですよね。だから、「この2つは表面上は違うけれども、構造上は同じものだよ」と言えないでしょうか。
大村:はい、言えます。
深沢:違うけれども同じ。「違うものを同じものとみなす道具なんだ」とはこういう意味です。
大村:なるほど。そういうことですか。
深沢:世の中的には「具体⇄抽象の思考法」なんて呼ばれるものですけど、数学にはこういう側面があるんですね。
大村:なるほど。抽象度を上げて物事を理解するみたいな話ですかね。
深沢:そうそう。だから、「構造化」みたいな頭の使い方が得意な方は、何か出来事があった時に、それを構造にして、「あ、このメカニズムの構造になっている別のものってこれがあるよね」と、別のものに置き換えることが上手です。
大村:なるほどね。
深沢:だから、例え話が上手かったり、他の業界の事例でものを説明できたり、別のものに置き換える人は(構造化が)上手な人。
大村:はいはい、「野球で例えると」とか、例えている人ってけっこう説明が上手な人が多いですよね。
深沢:その通りです。今大村さんは「説明上手」とおっしゃったじゃないですか。つまり今日の文脈でいうと、説明上手になるためには、「構造化」はとても大事な頭の使い方だということです。
大村:なるほど。
深沢:これが4番目。もうちょっとでおしまいですね。
大村:次が最後ですね。
深沢:はい、「モデル化」ですね。数学はモデルを作る学問です。

大村:三平方の定理。
深沢:はい。これはさっきおっしゃいましたよね。
大村:ラプラスの法則。
深沢:そうそう。数学って「ナントカの公式」がたくさんありますよね。
大村:等差数列、等比数列。
深沢:ありました。
大村:大嫌いです、僕。
深沢:嫌いなままでいいんです。大丈夫なので。
大村:大丈夫ですか。
深沢:大丈夫です。好きにならなくていいんです。ただ、こういう性質や特徴を「型」にして説明することが、数学の1つの特徴だということだけは、知っておいてもらえるとうれしいです。「ナントカの定理」「ナントカの公式」って、要はそのものの性質を説明しているんですよね。
大村:なるほど。
深沢:どうでしょう? あるものの性質を説明するって、数学の文脈を離れても、私たちの日常にたくさんあると思うんです。例えば「パレートの法則」なんて聞いてことがありますか?
大村:ああ、「2:8」でしたっけ。
深沢:はい。「ランチェスターの法則」とか。今日は会場にマーケティング関係の方もいますけど、ありますよね。要は、あれと同じことなんですよね。「こうなっていますよ」「こういう性質がありますよ」と説明しているものです。
大村:なるほど。
深沢:こういったものをうまく使うとコミュニケーションに大いに役立つというのが「モデル化」の話です。
大村:なるほど。
深沢:みなさま、よくがんばってついてきてくれました。数学って、この5つの動作でものを考える学問です。今日は「コミュニケーション」。「どう伝えるか」という話ですが、なんでこんなに時間を取って、考えるお話を2人でさせていただいたかというと、「思考が決まるから話し方も決まるのではないか」と思うからです。
大村:はい。考えてから話しますよね。
深沢:そうですね。考え方が決まるので、話す内容や言葉も決まるイメージです。
大村:なるほど。
深沢:例えば、すごく前向きに考える人、ポジティブな思考の人は、たぶん話し方もポジティブで、前向きな言葉がたくさん出てきますね。逆はたぶんネガティブな言葉がたくさん出てくる。それと同じで、ものを考える時の方法、考え方が決まるから、話し方も決まるのではないか。
ということは、さっきご案内した「数学的な思考」が身についていると、自動的に数学的な話し方になっているんですね。
大村:なるほど。
深沢:だからさっきの5つを身につけたほうが、みなさんにとって得なのです。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします
「コミュニケーション上手」=「説明上手」とは限らない 説明のうまい人がやっている「数学的思考」とは?
ビジネスで「例え話」がうまくなるコミュニケーション術 別のものに置き換えたり、事例で説明できる人の特徴
説明上手な人が口にする、本題に入る前の一言 なぜ上手い人が話すと「聞きやすい」「わかりやすい」になるのか
説明で相手に「確かにそうかもね」と思わせる人の共通点 正解のないビジネスで必要な「正しそうに伝える」スキル
フワッと話す相手から正しく情報を引き出すテクニック 伝え下手な人との会話で使えるスマートな質問術
話の内容がクリアになる、「一言」「1行」「1分」の提案術 言いたいことが相手に届く、説明のコツ