 PR
PR2026.01.19
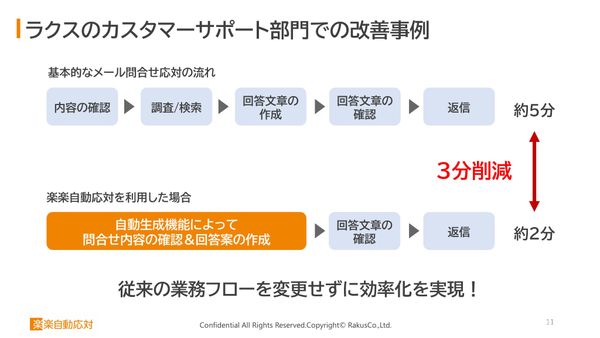
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
3 Ways Pi Can Explain Practically Everything(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
ハンク・グリーン氏:今週は様々なバックグラウンドを持つ人々が、宇宙で最も強力な事柄のひとつを祝うため特別な時を迎えます。そうπ(パイ)です。πは円の円周と直径の比率です。

これはコインのサイズから惑星のサイズま円の大きさに関わらず、その比率は常に同じであることを意味しています。また、πは非合理的であり、終わりがない上に反復もありません。しかし、πは3.1415から始まります。
そして、それが3月14日がPi Day(πデイ)と呼ばれる理由であり、今年のPi Dayは2015年3月14日ですから、日付は3-14-15となり数百年に一度しか起こらない数学的事象です。しかし、Pi Dayは数学をテーマにした焼き菓子を作ってお祝いする休日というだけではありません。
もし円や球に関連した勉強をしているならば、πを見たことがあるでしょう。科学者は、惑星の検知からから電界の測定や宇宙構造の説明まで、彼らの仕事上使用する円や球に多くの用途を見出しています。
自己紹介が遅れましたが、私はハンク・グリーンです。ここではπが全てを説明する3つの方法についてご説明します。最近、天文学者は太陽系内外の惑星への路を発見しました。彼らは惑星が主星の前を移動すると、その星の光の一部が遮られることからそれらの路を見つけることができました。そして、惑星が消えると星の明るさは通常に戻ります。
地球から見て光がどのように光っているかを示すグラフを光度曲線といい、この光度曲線をどのように解釈するかを理解するために、主星の大きさを知る必要があります。

では天文学者は地球上でどのように星の領域を把握しているのでしょうか? 球の表面積の方程式は、4πr²であり、rは星の半径を意味しています。
星の大きさを知ることが出来ると、その星が発する光がどのくらい変動しているのかを加味すると、惑星の大きさや大気中のものさえも把握できます。惑星の大きさを知ることは、その星に居住可能かどうかを推測するのに役立つので、πは惑星探査には必要不可欠な要素です。
つまり、球はまさに三次元で構成されているため、πは星のように球のようなものを勉強するためにはとても重要ということです。更に、私たちが物理学の力を計算する方法は、球とも深く関係しています。
例えば2つの電荷間の力である静電力を考えます。これはクーロン法と呼ばれる簡単な方程式を使って計算されています。空間の真ん中に浮遊している2つの電子があるとしましょう。各電子は全方向に力が作用しているため、基本的にその力は球を形成し、それを電界と呼びます。
しかし、これらの電界が反発しあって相互作用するとき、お互いが退け合うというだけの効果しか見られません。もしどのくらいの静電気力がそれらの電子を分離させようとしているのか計算したい場合は、目に見えない各電子の球が他の電子どれほど触れているのかを調べなければなりません。
そして、私たちは再び球体を扱っているので、もしろんそこにはπが必要になります。どのくらいの電界が接触しているかを理解するには、星の表面積を求めるのに使用したのと同じ式、4πr²を用いて両電子からの静電気力の合計を割り算する必要があります。
宇宙そのものを説明するためにπがどのように利用されたのかを話すことなく、化学におけるπの利用についての議論はできないとアルバート・アインシュタインが言っています。

アインシュタインは1世紀前の1915年に、一般相対性理論を発表しました。Pi Dayが3-14-15であった最後の時です。また、アインシュタインの誕生日はいつでしょうか? もしかして3月14日でしょうか? そう、彼はPi Dayに生まれました。
そして、アインシュタインの一般相対性理論は、運動のすべての形態とエネルギーがどのように時空を曲げることができるかを説明するためにπを必要としています。SciShow Space(番組名)では、星や銀河のような巨大な質量がどのようにして重力によって空間と時間を曲げることができるかについて、よく話しています。
しかし、アインシュタインの理論は、ちょうどベッドシーツの上にのっているボールのように運動やエネルギーのいかなる形態も、その周りの時空を曲げることができると言っています。そして、アインシュタインがその事実を説明するのに使った方程式はπを使っています。

この方程式は基本的に物理的世界を定義しているので、その中で多くのことが起こっています。しかし、重要なポイントの1つは、重力、運動、エネルギーの関係を説明する固定比、定数があるということです。
そして、アインシュタインは「場の理論」の観点で物理学について話していたので、πはその定数の一部でなければなりません。電子のように物体の小さな各部分は、あらゆる方向に独自の重力場を生成し、一緒になってその物体の周りに力の球状領域を形成します。
そして、球があるところには、πがあります。このような重要な数字のため、πは公式のお祝いが1年に一度しかないことの悲しいことであり、特に特別な今回のような日は2115年まで現れません。
しかし、いかなる時も世界のどこかで、何か重要なことにπを使っている数学者や科学者がいるということは確かです。
 Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル
Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします