 PR
PR2026.01.19
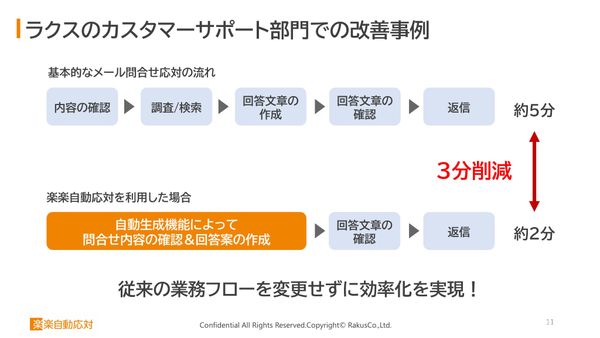
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
Game Theory: The Science of Decision-Making(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
ハンク・グリーン氏:友達といるときには、あなたの下した決断の先にある数学について考えることはあまりないかもしれませんが、社会的なやりとりに関連する数学理論が存在します。それは「ゲーム理論」と呼ばれるものです。
ゲーム理論は1950年代に数学者のジョン・ナッシュにより提言されました。ラッセル・クロウが『ビューティフル・マインド』で演じた彼です。

ゲーム理論は、普段私たちがゲームに対して持っているイメージとは違い、利益が他人の判断により決まる複数の人間によるやりとりに関するものです。ポーカーにも同じことが言えます。それに、やはり人が集まりビジネスが交差する場所でもそれは言えるのです。
あなたは最近、誰かとやりとりしましたか? したとすれば、おそらくその判断はゲーム理論によって分析できます。
ゲーム理論の幅は広く、経済学者、科学者、生物学者、軍事戦略家、心理学者などにも使われてきました。
ゲーム理論には2つの思考があります。協力的か非協力的かということです。非協力的なゲーム理論は競争的なやりとりを司ります。そこには勝者と敗者がいます。おそらくもっとも有名な思考実験として、囚人のジレンマが挙げられます。

囚人のジレンマは、2人の囚人による社会的なやりとりを意味します。ワンダとフレッドとでも呼びましょう。2人は逮捕され、2年間、刑務所の中で過ごさなくてはなりません。しかし検事はそれ以上を求めています。そこで彼は2人にある条件を提示します。
自分が犯行を認めて、パートナーが認めない時は服役を免除、つまり刑務所から出られる。しかしパートナーは10年刑務所に入る。
お互いに犯行を認めてパートナーについて白状するなら、2人とも5年で済む。
どちらも認めなかった場合、両方2年刑務所に入る。
という状況です。ワンダとフレッドは離ればなれで、お互いがどうするかを知ることができないため、1人で判断しなければなりません。2人は一緒にダイヤモンドを盗むなどした仲ですが、忠誠心があるわけではありませんし、兄弟でもありません。お互いが裏切ることがあっても不思議ではありません。
競争的なゲーム理論は彼らの選択を調整し、結果を一定のグリッドに落とし込みます。

お互い犯行を認めない場合、2年。理論上これがベストです。可能な限りの短い期間です。しかし免除はいい話なので、告げ口を顧慮するとこうなります。2人はお互いを信じる理由はありません。
お互いに犯行を認めなければ彼らにとってベストですが、フレッドが告げ口するかどうかはワンダはにはわかりません。告げ口はフレッドにとって得だからです。ワンダが掛けて黙ったとして、刑務所に10年入るリスクがつきまといます。
それに比べると、お互いについて白状することはそんなに悪くはなくなります。これが、ゲーム理論の結果なのです。お互い犯行を認めるということになるのです。
ゲーム理論はたちが悪いと思った人もいるかもしれませんが、実はこれは理にかなったことなのです。あのグリッドが、ナッシュ均衡に達した結果なのです。

これは競争的なゲーム理論でキーとなるコンセプトです。相手の判断に関わらず、自分に取って都合のいい結果となる選択をした時、プレイヤーはナッシュ均衡に達しているのです。
ワンダが犯行を認め、フレッドがそうしない場合、彼女はうまくいきます。懲役2年から免除にすらなります。そこでフレッドが犯行を認めても、まだ大丈夫です。黙っていれば、10年ですが、5年で済むからです。
お互い認めないと約束したなら2年で済みますが、それは確信できません。なぜならワンダにはフレッドの行動が読めないからです。
これは協力的なゲームではありません。すべてのプレイヤーは裏切ることによって利益があるからです。囚人のジレンマは例の1つですが、基本的思考はどの状況にも当てはまります。
一般的に、他人と競争する場合、他人がどうであれ自分に有益な判断をします。そこで協力ゲーム。共同ゴールへの共同作業のためにみんなが賛成します。
レストランでグループの会計をするときから、温暖化対策で集う国家間においても同じことが言えます。ゲーム理論では、提携が可能な状況は「協力ゲーム」と呼ばれます。プレイヤーがどれだけ提携に貢献し、利益を得られるかが問われます。それと同時に、なにがフェアかも問われます。
競争的ゲーム理論にナッシュ均衡があったように、協力ゲーム理論にシャープレイ値があります。シャープレイ値はプレーヤーの貢献度に応じて利益やコストをプレーヤーで分配します。いくつかの原理を適応するとそれが働きます。
1つ目、各プレーヤーの貢献は、そのゲームから本人を省いた場合の損得で決められる。これをマージナル・コントリビューションと言います。例えば友人とクッキーを作るとしましょう。自分が病気になった場合、作れるクッキーが50枚減ったすれば、マージナル・コントリビューションは50となります。
2つ目、交換可能なプレーヤーは同じ価値になります。提携に同じものをもたらすなら、同量を貢献し、同量の報酬を得ます。レストランで2人が同じものを頼んだら、2人とも支払う額は同じ、ということです。2人の同僚は、同じ賃金であるということです。
3つ目、役に立たないプレーヤーの価値は0です。つまり、貢献しなければ、なにも受け取らないということです。これは議論を醸しています。
友人とレストランに行き、自分がなにも頼まなかった場合、お会計の時にチップを払わなくていいというのはフェアに聞こえます。しかし職場で貢献できない場合、対価を受け取るべきではないとも言えます。貢献できない正当な理由もあります。育児や事故などです。その場合にも提携は分け前を与えます。
4つ目の原理です。ゲームに複数のパートがある場合、支払いはパートにより分割されるべきということです。例えば月曜はたくさん働いて、火曜はのんびりした場合、それぞれの報酬は別だということです。サラダを頼んだ日とステーキを頼んだ日とでは、ステーキにより多く支払うということです。
つまり、同じ策を毎回使うことがフェアではないということなのです。提携が調整できるようにするため、数値は定期的に改正されるべきであるということです。コストを分け、すべてのプレーヤーが満足しすべての原理を満たす、これがシャープレイ値です。
シャープレイ値は数学的にこのようにも表現されます。複雑ですが。

数学っぽくないコンセプトにすることも可能です。クッキーの話に戻ります。

あなたと友人がクッキーを焼く。あなた1人だと1時間10枚のクッキーが焼ける。しかし友人は1人で20枚焼けます。そこで、製造ラインを統合して協力すれば、1時間で40枚のクッキーが焼けるとします。お互いの協力なしでは30枚しか焼けません。

1枚1ドルで売るとして、40ドルの稼ぎになります。そこで、どう利益を分けるか。シャープレイ値の説明はこうです。
あなたが1時間10枚焼けたとして10引くと、友人に30が残ります。友人のマージナル・コントリビューションは30です。1時間に20枚焼ける友人が、40から20を引くと20となり、あなたのマージナル・コントリビューションが20となります。
当初、あなたの価値はクッキー10枚でしたが、協力することで20枚になったのです。シャープレイ値によると、2つの数字を平均しなければいけません。つまりあなたは15ドル、友人は25ドル得ることになります。
各自のマージナル・コントリビューションを見つけ、数百人ものプレイヤーの提携に適応することもあります。囚人のジレンマやクッキーよりはよりはややこしくなりますので、ゲーム理論はそれ以上のものがあると言えます。
そこでこう結論します。ゲーム理論とは、競争的な環境で、いかにスマートになれるかを教えてくれるのです。そして協力的環境では、いかにフェアであるべきかということを教えてくれます。
 Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル
Hank Green(ハンク・グリーン)たちがサイエンスに関する話題をわかりやすく解説するYouTubeチャンネル。 ・公式チャンネル続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします