 PR
PR2026.02.26
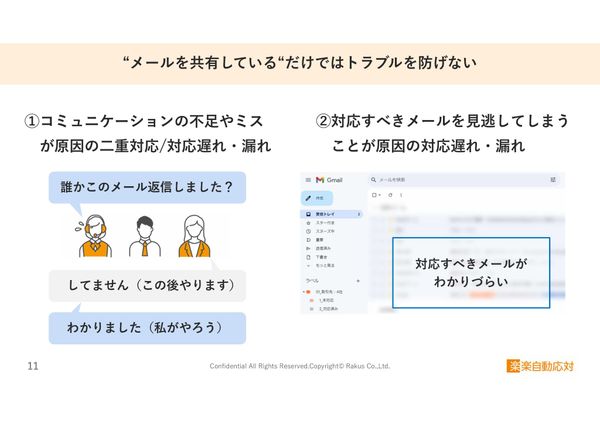
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
『原論』の魅力を語りたい(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
キグロ氏:私の発表は動画なので、さっきのようなこと(スライドの表示の不具合)は起こりえません。
(会場笑)
逆に言うと動画なので、ちょっとでもとちると全部失敗しますので、とちらないように祈っていてください。では、よろしくお願いいたします。
(会場拍手)
日曜数学会のキグロと申します。(スクリーンを指して)あんな感じのアイコンでTwitterやニコニコ動画をやってるので、ぜひ見てください。よろしくお願いします。

私の発表は、「『原論』の魅力を語りたい」というものです。『原論』ってそもそもなんやねんって話からしたいんですが、たぶん知ってますかね。紀元前300年ごろにアレキサンドリアのユークリッドという人が書いた数学の教科書だといわれています。全13巻からなり、幾何学、代数学、数論などを幅広く扱っている本です。
現代でも普通に本屋で買えます。(現物を見せて)これ。6,000円プラス消費税です。

(会場笑)
ちょっと高いですけど、でもみなさん、いまさらっと説明したんですけど、よく考えてくださいよ、2,300年前の本が今でも普通に買えるって、これめちゃくちゃすごくないですか? 聖書より古いんですよ?
(会場拍手)
で、いったいなにがそんなにすごいのか、なんでこんなにロングセラーになっているのかっていうのを語りたいんですが、すごいところがいっぱいあってですね、100π秒で話すのはムリです。ということで今日はテーマを絞って、「数」についてちょこっと語りたいなと思います。
で、さっそくですがこれ、原論に出てくる挿絵の1つです。

なにかを説明している図ですけれども、いったいなんの説明図かといいますと、有名なユークリッドの互除法の図なんですね。

ふーんって感じなんですけど。
(会場笑)
もう1ついきましょうか。こちらはどうでしょうか。

見てみますと、これもなにかを説明しているんですが、なにを説明しているのかというと、素数の無限性、つまり素数が無限個あることの証明の図なんですよ。

さっきのユークリッドの互除法も素数の無限性の証明も、現代だったら図なんて使わないんですよ。整数論の話なんで数式書けば済む話なんで、わざわざ図なんて書く必要はないんですね。にもかかわらず、原論ではこうやって図を使っているんです。
というのも、原論では数を線分として表しているんです。この2つに限らず、いろんなところで数が線分として書かれているんです。
なんでかって言うと、当時は数っていうものを「長さ」であるという認識をしていたんですね。なので数を説明するときに、必ず図も入っていた。そのため使われている語彙も図形と共通のものがかなりたくさんあるんです。
例えば、三平方の定理。現代のわれわれが文章で書こうと思ったら、たぶんこんな感じになると思います。「斜辺の2乗は、ほかの2辺の2乗の和に等しい」。まあ、こうですよね。
これが原論ではどう書かれているかといいますと、「直角の対辺の上の正方形は、直角をはさむ2辺の上の正方形の和に等しい」というふうになっているんです。

ちょっと長くなっているんですけど、ポイントはこの「正方形」という部分。要するにこれ、2乗のことを正方形って書いているんですよ。まあ、2乗っていう言葉がないわけじゃないんですけども、しばしば2乗のことをこうやって正方形っていうふうに表現しているんですね。
ほかにもいろいろありまして、例えば「AとBの積」のことを「AとBに囲まれた矩形」、矩形っていうのは長方形のことなんですけれども、こういうふうに表現している。つまり、AとBを辺とする長方形の面積がAとBの積であるという認識をしている。
このほかにも、Aの平方根のことを「Aの辺」って書いてますね。つまり、面積がAの正方形の、1辺の長さがAの平方根であるという考え方をしている。ちなみに当時、マイナス・負の数がないので、Aの平方根っていうのは正だけです。
もう1つ具体的にいくと、2つの数を掛けた数のことを「平面数」って言ってます。当然3つの数を掛けると、今度は「立方数」っていう言い方になる。こんな感じで、図形と共通の用語をたくさん使っているんですね。
さらに言うと、実は当時、数式がなかったので、現代なら数式で書くようなこともずっと図で書いていたんですよ。例えば、こちら。

ある有名な公式を表している図なんですけども、なんの図かっていうと、これです。

この展開の公式。現代のわれわれは、この展開を数式で暗記するわけですけれども、当時これを使って勉強していた学生たちは、あの図を暗記していたというふうに言われているんです。
では、こちらはどうでしょうか。

これ、かなり難しいんですが、この二次方程式の解なんです。つまり「x=(-a+√5a)/2」を表している図なんですね。

現代のわれわれだったら、二次方程式の解の公式を暗記しているわけですけれども、当時の学生はあの図を暗記していたと。あれが2次方程式の解の公式だったんですね。
こんなふうに、原論には現代ではあまり使われていない考え方っていうのがすごくたくさん出てくるんです。いまの数以外にも。
で、そこから2,000年以上の長い年月をかけて、いまのわれわれが持っている概念・考え方・表記法などなどが少しずつ形成されていったということで、結論。
「『原論』を読んで数学の歴史を感じよう!」ということで私の発表は以上です。ありがとうございました。
(会場拍手)
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします