 PR
PR2026.02.26
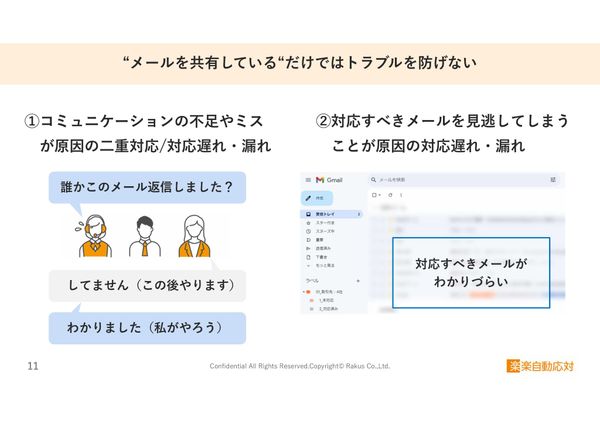
メール共有しても二重対応や漏れ・・・ コールセンターの悩みを解決する「楽楽自動応対」の4つの機能
まろやか巨大数 グラハム数を超えた世界(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
司会者:漫画家の小林銅蟲さん! お願いいたしまーす!
(会場拍手)
小林銅蟲氏(以下、小林):どうも。もうやるんですか?
(会場笑)
小林:よろしくお願いします。今日は、「まろやか巨大数。グラハム数を超えた世界」というテーマで、お送りしようと思います。
どうも、こんにちは。僕はなんなのかと言いますと、小林銅蟲という漫画家で、今は、MANGA pixivで数学の漫画とイブニングで料理漫画をやっております。よろしくお願いします。
今日は、巨大数というものについてお話をするんですけれども、非常にざっくりした感じでいかせていただきます。みなさん、巨大数を知っているかどうか、わからないですけども。要するに、すごく大きい有限の数。

ここにいっぱい、大きめの数が並んでますけど、実際、僕とか、ほかのファンの方が扱っているのは、もっと大きくて、宇宙の原子を全部使っても書けないような数です。
そういう、数が大きければ大きいほど、興奮する人たちがいます(笑)。僕も10年くらい前から興奮してるんですけれども。
(会場笑)
可能な限り大きな巨大数を作って眺めると。可能な限り。有限の数というのは、有限だからいくらでも大きくできるんじゃないのっていう話なんですけれども。
大事になってくるのは、どうやってものすごく大きい数を作るかという、その仕組みのほうにウェイトがあるんですね。どういうふうに作るか。要するに、原料を、3とかを巨大数を作る関数、生成器に入れるとでっかい数が出てくる、というのがメインストリームです。

要するに、大きな数を作るには、より強力な関数、生成器が必要だということになるんですね。当たり前ですけど、弱い関数では、強い関数に絶対勝てない。例えば、2xというのは、2のx乗に対して増加速度では絶対勝てない。こういうことが上のレベルでも起こってくるんですね。
日本とか海外でみんなやってるんですけど、みんなが各々勝手な方法で作ってくるので、どうやって関数の強さを比較したらいいのかというのが、けっこう長い間なかったんです。でもここ数年できてきました。比較用の関数というのがあるんですね。
その関数を、仮に、fn(x)と言うんですけども、この添え字のnの数が大きければ大きいほど、その関数は強いと言えるんですよ。例えば、x!(xの階乗)の関数は、f2(x)くらいだと。強さは2だと。

これに対して、超冪(ちょうべき)という、aのa乗がx個並んだような関数。これが、f3(x)くらいの強さなんですね。

わりと有名な巨大数で、グラハム数という非常に大きな数があるんですけれども。グラハム数を作ることができる関数というものの強さがどれくらいかというのを、さっきのfn(x)で表せるんですけど。これはですね、fω+1(x)であると。
(会場笑)

ωってなにか、と。
(会場笑)
ご存知の方もいるかと思いますが、無限ででてきますね。さっき有限だっつったのに、いきなり無限がでてきたんですけども。
(会場笑)
なんでかと言うとですね。我々、有限の巨大数を作るんですけれども、方法論として、機械に無限を突っ込むと有限の巨大数が出てくるというタイプの関数があるんですね。

さっき使ってるものさしの関数もそうなんですけれども。そうやってやると強いと。
無限にもいっぱい種類があって、それぞれ序列が決まっていたりもするので、より強い無限を生成器にぶち込んでやると、でっかい数が出てくるという通りがございます。
グラハム数に勝とうとした日本人がいまして、グラハム数よりでかくするだけのために作っただけの数という。とにかくでかいだけが取り柄の数。これがバージョン7まであるんですけど。
(会場笑)
さっきのグラハム数の強さが、ω+1でした。このふぃっしゅ数バージョン1が作れる関数の強さは、だいたいfω^2+1(x)くらい。

明らかに強いと。
(会場笑)
バージョン2になるとですね。fω^3(x)になります。

バージョン3になると、f(ω^ω+1)63+1(x)くらい。

ちょっと飛んで、バージョン5は、fε0+1(x)。

これも無限なんですけど、強さ的にはこういう強さですね。

(会場笑)
もちろんこのε0の上にも無限があって、階層がなんぼでもあるんですね。なんでこんな上の無限の話ばかりしてるかと言うと、いまどき、みなさんが作る巨大数がでかすぎて評価が大変だと。
とにかく、強さが全部無限の世界に入ってるんですね。表記できるのが。無限同士で強さを測らなくちゃいけないから、上の無限をいっぱい知ってなきゃいけない、扱えなきゃいけないという話になっちゃうので。最近、そのまま使えないような、わけわからないような無限とかも使えるようになってきているんですね。
さっきのωとかは、可算の順序数なんですけど、最近、非可算のやつとか巨大基数とか突っ込んできてる人たちがいて、非常に怖いんですけれども。
(会場笑)
今まで言ってきた巨大数に使う関数というのは、だいたい計算可能な関数で。そういう定義があるんですね。計算可能であるという。計算可能でない関数というのがあってそれを使うことによって、計算可能なものよりも常にでかい巨大数と関数が作れるんですね。
そういうわけで、巨大数業界の上のほうにいくと、わけわかんないやつがいっぱいいるんですよ。今回、そのわけわかんないやつの話をざっくり紹介しますと、「ラヨ数」というものがありまして。

定義書いてありますけど、長いんですね。要するに、ある数学の理論体系で表現できる一番でっかい数みたいな定義なんですね。
もちろん計算不可能なんですけど、これがけっこう長い間1位を占めていて、どうにか勝とうと思ったのが、やっぱり日本人で、ふぃっしゅ数バージョン7という。
(会場笑)
がんばって、プロセスをいじって強くして上回ったんですね。そしたら、また、外人ががんばって、ラヨ数を構成する論理体系自体を拡張して、さらにでかいのを作っちゃって。

ちょっと今、これよりでかい名前が付いている巨大数ってないんですね。今のところ、ビックフットが最強です。
そういう感じなんですけど。今のトピックというのが、今までのざっくりな感じで、数学の理論体系の強さ自体を巨大数に変えて殴り合っている状況というのがあります。
(会場笑)
けっこうえらいことになってるんですけども。そんなわけで、最上位の巨大数の話というのは、普段あまりできないので、(いつもは)もうちょっと下のほうの話をご紹介してるんですけど、今回無理やり、ご紹介しました。
それで、抜け落ちたお話がいっぱいございますので、インターネットで見ていただきたいものがいろいろございます。みなさま、おもしろい分野なので、ちょろっと触ってみたらいかがかなと思いますけれども、今回はこれで、終わりでございます。
ありがとうございました。
(会場拍手)
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします