 PR
PR2026.01.19
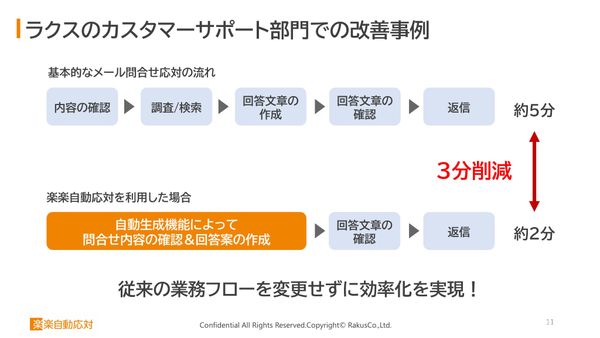
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
How to Predict the Odds of Anything(全1記事)
コピーリンクをコピー
ブックマーク記事をブックマーク
ハンク・グリーン氏:未来について預言できるようになりたいとは思いませんか? 残念ながらそれはできません! ところが、多くのお金と人々の生活が、日々、未来の事象を科学的に予測することに依存しているのです。
選挙の結果予測からハリケーンの威力、テロ攻撃の可能性にいたるまで、私たちは統計的分析に基づいて予測し、それによってリスク評価やお金の投資をし、人生を決定づけるかもしれない決断を下しています。
しかし、本来知る由もない未来の出来事の確率を、どうやって予測すればいいのでしょうか? 次のケースについて考えてみましょう。
ここに、自分が乳がんかどうか知ろうとしている40代の女性がいるとします。統計によれば、もし彼女が乳がんである場合、マンモグラフィによって陽性と診断される確率は75パーセントです。

一方、彼女が乳がんでなかった場合、マンモグラフィが誤診をして陽性と判定してしまう確率が10パーセントあります。つまり乳がんでもないのに、乳がんであると診断されてしまう確率です。
また、40代の女性の1.4パーセントが乳がんを患っています。この女性がマンモグラフィを受けた結果、乳がんであると診断されたとします。さて、このテスト結果が正しい確率を求めてください。ほとんどの人が「75パーセントくらいだろ?」と考えるのではないでしょうか。
間違いです。彼女が実際に乳がんを患っている確率は、たったの9.6パーセントです。不正解のあなた、恥じることはありません。ほとんどのお医者さんが同じ間違いを犯すのですから!
このような間違いを防ぐために「ベイズ推論」が存在します。私たち人間の直観的な考えとは相反するベイズ推論ですが、実は多くの現代科学の考え方の基盤となっています。

ベイズ推論は、ある仮説を証明あるいは反証しようと試みる際に、特定の情報(注:実験結果など)がどれだけ信頼に足るかを見極める方法論です。ベイズの定理によれば、そのためには次の3つの要素が必要になります。
まず、実験や調査を行う前に、あなたが立てた仮説が正しい確率を知っておく必要があります。今お話ししているケースの場合、「マンモグラフィの検査を受けたとき、この女性は乳がんだった」というのが仮説になります。
次に、もしあなたの仮説が正しい場合、この実験によって仮説通りの結果が得られる確率を知っていなくてはいけません。
このケースでは、マンモグラフィという検査によってこの女性が乳がんであると診断される確率です。
最後に、あなたの仮説が間違っていたにも関わらず、あなたの仮説通りの結果が実験によって得られる確率です。つまり、この女性が実際は乳がんではないのに、マンモグラフィによって乳がんであると診断される確率です。
初めてこのケースに直面する多くのお医者さんが間違いを犯すように、あなたもきっと、マンモグラフィによって陽性と診断されたということは、75パーセントの確率で乳がんだと考えることでしょう。
それは「乳がんの女性が陽性のテスト結果を得る確率」と「陽性のテスト結果を得た女性が実際に乳がんである確率」が同じである、と考えるからです。これは私たち人間が陥りやすい典型的な間違いです。
この2つの確率は同じではないのです! それどころか、まったくもって、途方もなく違う確率なのです!
ベイズ推論に基づいて、次のように考えてみましょう。40代の女性を1000人集めたとします。このうち、14人が乳がんを患っていますよね。40代の女性の1.4パーセントが乳がんを患っている、という統計をご紹介したのを覚えていますか? それはつまり残り986人の女性は乳がんではないということを意味しています。
この乳がんを患っている14人の女性がマンモグラフィを受けて陽性と診断される確率は75パーセントです。14人の75パーセント、つまり10.5人です。一方、乳がんでない986人がマンモグラフィを受けて陽性と診断される確率は10パーセントです。986人の10パーセントは98.6人。
つまり1000回のマンモグラフィのテストを行った結果、10.5人に「真の陽性」結果が、98.6人に「偽の陽性」結果が下され、あわせて109.1人の女性が陽性という診断を受けることになります。
この109人のうち、本当に乳がんを患っているのは10.5人。ということで、「40代の女性で、マンモグラフィのテスト結果が陽性であった人が本当に乳がんを患っている確率は9.6パーセント」という確率が導き出されるわけです。
私たちはふだん、こんなふうに物事を考えたりしませんよね。しかしこれこそが、実験結果が現実に有意(注:確率的に偶然とは考えにくく、意味があるとみなされること)であるかどうかを図る唯一の方法なのです。
ベイズのように考えないと、自分が導き出した事象の妥当性を途方もなく過大評価してしまう危険性があります。実際、これが自然科学の大きな問題でもあるのです。アメリカの学術論文に記載されている実験結果の80パーセントが、再現不可能であるという事実がそのよい例でしょう。
ベイズ推論は、私たち人間が時に苦手とする「論理的に思考する」のを助けてくれます。より論理的に思考することは、より優れた自然科学を生み出すのです。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
関連タグ:
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします