日本の教育の問題点は、子どもの「当事者意識」を奪うこと 教育者・工藤勇一氏が考える、今の学校教育に足りない視点
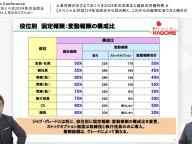
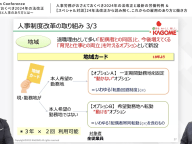
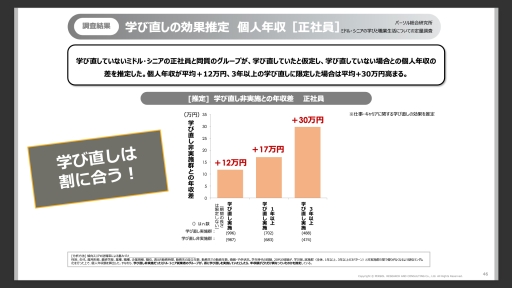
1人2回まで、絶対に希望勤務地で働けるカゴメの人事制度 社員自らキャリアを選び取るための「働き方のオプション」の必要性
エール篠田真貴子氏が明かす、経営陣ゆえの時間管理の難しさ 『LISTEN』発売時に経験した、多忙な日々の中で感じたこと
編集部のオススメ

How Teams Can Skip the Drama and Embrace Healthy Conflict #4/4
Bad Workplace Culture is Giving Burnout #4/4
How Teams Can Skip the Drama and Embrace Healthy Conflict #3/4
Bad Workplace Culture is Giving Burnout #3/4
How Teams Can Skip the Drama and Embrace Healthy Conflict #2/4
Bad Workplace Culture is Giving Burnout #2/4
Bad Workplace Culture is Giving Burnout #1/4
How Teams Can Skip the Drama and Embrace Healthy Conflict #1/4
The DNA of a Unicorn Leader #5/5
The DNA of a Unicorn Leader #4/5
The DNA of a Unicorn Leader #3/5
Five Ways to Improve Well-Being in the Workplace: Emerging Trends from the Science of Happiness #5/5
Why Awkwardness is Your Best Asset for Risk-Taking at Work #4/4
The DNA of a Unicorn Leader #2/5
Five Ways to Improve Well-Being in the Workplace: Emerging Trends from the Science of Happiness #4/5
Why Awkwardness is Your Best Asset for Risk-Taking at Work #3/4
The DNA of a Unicorn Leader #1/5
Five Ways to Improve Well-Being in the Workplace: Emerging Trends from the Science of Happiness #3/5
Why Awkwardness is Your Best Asset for Risk-Taking at Work #2/4
Five Ways to Improve Well-Being in the Workplace: Emerging Trends from the Science of Happiness #2/5
Why Awkwardness is Your Best Asset for Risk-Taking at Work #1/4
Culturally Confronting Loneliness #3/3
Five Ways to Improve Well-Being in the Workplace: Emerging Trends from the Science of Happiness #1/5
Culturally Confronting Loneliness #2/3
AI and Humanity’s Co-evolution with OpenAI’s Head of ChatGPT #4/4
Culturally Confronting Loneliness #1/3
Business, Life, and the Magic of Austin: A Conversation with Michael Dell #3/3
Life After Big Tech - Where Are Laid Off Workers Now ? #4/4
AI and Humanity’s Co-evolution with OpenAI’s Head of ChatGPT #3/4
Business, Life, and the Magic of Austin: A Conversation with Michael Dell #2/3
Life After Big Tech - Where Are Laid Off Workers Now ? #3/4
AI and Humanity’s Co-evolution with OpenAI’s Head of ChatGPT #2/4
Business, Life, and the Magic of Austin: A Conversation with Michael Dell #1/3
Life After Big Tech - Where Are Laid Off Workers Now ? #2/4
AI and Humanity’s Co-evolution with OpenAI’s Head of ChatGPT #1/4
The Singularity Is Nearer #3/3
Life After Big Tech - Where Are Laid Off Workers Now ? #1/4
The Singularity Is Nearer #2/3
How to Differentiate Yourself as an Entrepreneur #4/4
The Singularity Is Nearer #1/3
How to Differentiate Yourself as an Entrepreneur #3/4
Featured Session 10 Breakthrough Technologies of 2024 #3/3
How to Differentiate Yourself as an Entrepreneur #2/4
Featured Session 10 Breakthrough Technologies of 2024 #2/3
How to Differentiate Yourself as an Entrepreneur #1/4
Featured Session 10 Breakthrough Technologies of 2024 #1/3
新着ログ
人気ログ