 PR
PR2026.01.19
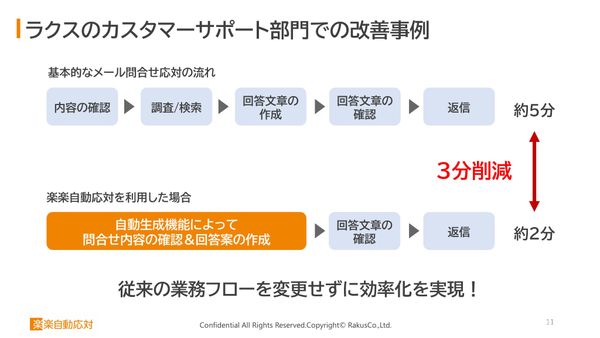
業務フローを変えずに、メール1通3分を削減 自動でAIにナレッジが貯まる問い合わせシステム「楽楽自動応対」
コピーリンクをコピー
ブックマーク記事をブックマーク
エディットプラン合同会社が主催した「親のためのリベラルアーツ入門」をテーマとしたイベントに、新刊『自分で考える力を鍛える 正解のない教室』の著者で、探究型学習の第一人者の矢萩邦彦氏が登壇。編集者・松岡正剛氏の弟子でもある矢萩氏が、「自分軸」を持ちづらいワケや、受験のために合理化のデメリットなどを語りました。
矢萩邦彦氏(以下、矢萩):私は大学院で「実践リベラルアーツ論」を担当していますが、「リベラルアーツ」と「実践」は、日本においてはけっこう相反するというか、一般的には「すぐに使えるものではない」というイメージがあるんですね。
でも、そんなことはないんですよ。リベラルアーツはいくらでも実践できます。何を実践するかと言うと、先ほどから申し上げている「選択」です。人生において自分で「選択」をしていく。その選択の判断基準、自己決定の基準になるものがリベラルアーツです。
じゃあ何を自己決定の基準にしていけばいいのか。私は(スライドの)この3軸が重要だと思っています。

まずは古典的なリベラルアーツで大事にされている「世界の基本構造」ですね。法則や科学の世界のことなのか、法律や文化なのか、規律やルールなのか。そうやって、情報を階層で分けて考えます。
法則の世界のことは、自分ではどうしようもないから、悩んでもしょうがない話ですよね。でも、法律や文化は場所が変われば変わるから、今いる場所が合わなければ引っ越すこともできるし、自分で提言して社会を変えていくこともできるかもしれない。
組織の規律やルールだったら、もっと規模が小さいですから、もっと変えやすいかもしれない。別の場所を探すのも簡単かもしれない。このように情報の仕訳をしていくことが、まず第一です。
あとは言語をしっかり使えるようにするとか、論理的に考えるとかね。従来の学校教育の中で一応やろうとしていたことは、この「世界の基本構造」にあたります。
ただ、最も抜けているものの1つが、この「自分軸」です。なんで自分軸が抜けてしまうかというと非常に簡単です。学校教育では「みんな違ってみんな正解」とはできないんですよね。どうしても評価しなければいけない。そして公平に扱わなければいけないので、どうしても公平に採点しやすい問いを日常的に扱うことになる。
一問一答的な、正解が存在する問いしかやらないんですね。そうすると模範回答が存在して、〇か✕かがはっきりつけられるようなことばっかりになってくる。でも世の中には、正解が存在しない問いは、たくさんあるはずです。
例えば、答えが1つではない場合もあります。答えが存在するかどうかすらわからないミステリーもありますし、答えは必ずあるんだけれども、誰か、あるいは何かによって隠されているものもあります。
いろんな問いがある中で、学校では一問一答のものばかりをずっとやり続けているんですね。すると「私はこれを信じているからこれが答え」とか、「私はこっちのほうがいいと思います」とか、美しい・美しくないとかの評価軸がなかなか育ってこない。
そんな環境に10年以上いるんですよ。いきなり総合型選抜だとか就活だとかが始まって、「あなたの自分軸を書け」と言われても、今までそうでないところだけを評価されてきたのに、混乱してしまうというか。自分勝手なことを書くなとか、言うなとか、言われ続けているので、何を言えばいいんだかわからなくなってしまいますよね。
なので、ここを学校教育の現場で、すぐに身につけるのが難しいのであれば、やはり家庭、あるいはその他の民間とか、どこでもいいんですけれども育むこと。そういう環境作りを考えていくことが今は急務だろうなと思います。
あとは、「最新の世界観」を把握することですね。これも学校現場では非常に難しい。学校は教科書を使ってるんですよ。教科書は作成に非常に時間が掛かるんですね。みんながこれは正しいもの、これは必要なものと合意形成をしていって、もう何年も何十年もかけてできているものです。
だから「世界がいきなり去年こう変わりました」とか、「今年こんな新しい技術ができました。じゃあ教科書を変えましょう」みたいに簡単なことはできない。構造的に、最新の世界観を反映できないんです。
でも、我々は最新の世界観の中で生きているんですよ。今、ICT技術のことを無視して就活なんか考えられないです。もちろん学校でも、がんばって対応しています。私立なんかはかなり先進的なことをやっていたりもしますけど、やはり一枚岩ではない。すべての先生が同じ感覚ではないわけですね。というわけで、これらを考えることが非常に重要かなと思っています。
ちょっと見方を変えると、「世界の基本構造」はこの世界のトリセツ(取説)みたいなものです。

「最新の世界観」は現状のマップです。その中でプレイヤーとしての自分がいったいどんな選択をしていくのか。ここは自由ですよね。オープンワールドみたいな感じです。
でも自由に歩いて得をするか損をするか、どんな選択肢があるのかをわかるためには、やはりこの(スライドの)下の2つ。「基本構造」と「世界観」を知っていく必要がある。ここに私は現代の実践リベラルアーツの、一番大事な部分が集約されていると考えています。
おまけの話をしておくと、最近「探究」「アントレプレナーシップ」、そして「リベラルアーツ」の3つの言葉が、教育界で散々キーワードとして上がってきます。この3つは、けっこういろんな解釈をする方がいるので、わかりにくくなっているんですけれども、簡単にまとめるとこういう感じです。
「リベラルアーツ」とは、主体性を軸にした「方法」です。主体性を軸にした「精神」が「アントレプレナーシップ」。そして主体性を「実践」するのが「探究」になります。
自由選択と自己決定のための知識・技術がリベラルアーツ。主体的な実践や活動・学習・経験のことを「探究」活動という。そして主体的であろうとするマインド。別に起業家精神ではないんですよ。起業しなくたっていいんです。自分でそうしたいと思ったことをやる。自分で選択できるんだというマインド。それが「アントレプレナーシップ」です。
というわけで、全部の共通項は「主体性」です。この「主体性」のど真ん中にあるのが、先ほど出てきた「自分軸」になりますね。「あなたはどうしたいの?」「あなたは何ができる?」「何を学びたいの?」「何をやってきたの?」。全部主体の話です。
これはもう全員が違っていいし、解釈も違っていい。これらがあまり身についてこない、従来型の教育の問題点は、いったいどのへんにあるのか。これを見てみたいと思います。もちろん全部を話すわけにはいかないので、非常に抜粋した抽象的な話にはなるかもしれません。
これは、2010年に文科省が発表した「生きる力」というパンフレットで紹介されたものです。「次の平行四辺形の面積を求める式と答えを書きましょう」という問題があります。

これが知識型の問題ですね。
「活用型の問題」と分類されていたのがこれ。「この公園とこの公園、どっちの面積が広いですか」。

やることは同じですよね。四角形の面積が求められるかどうかです。この公園は長方形なのでここ(長辺)掛けるここ(短辺)ですよね。この公園は平行四辺形なので、知識型の問題と同じ求め方でできるわけです。
さて、どれぐらい正当率に違いがあったのかを想像して欲しいんですが、実は①の正当率は96パーセント。ほとんどの小学6年生が答えられた。ところが②の正当率は18.2パーセントしかなかったんですよ。

つまり平行四辺形の面積を求める力が、平行四辺形の面積の問題でしか活用できてないんです。そこでしか発揮できていない。ぜんぜん応用・転用ができていない。このあたりが非常に、現代の学習の問題点と言えると思います。もちろん、文科省も問題点に気がついて、それをなんとかしようという改革の流れが今に続いているわけです。
切り取ってしまうと「文脈」が失われるんですよね。先ほども平行四辺形を切り取ってそれをトレーニングしていると、どうしても平行四辺形だけしか見えなくなってしまう。「何ごともできる限りシンプルにすべきだが、必要以上に単純化してはならない」のは、アインシュタイン(アルベルト・アインシュタイン)さんが言ったことですけれども。
なんでこんなことが起こっているかというと、時間が決まっているんですよね。限られたカリキュラムの中で入試の出題や教科書を網羅しようとします。これは塾業界も同じです。そうすると合理化が必要になってくる。どうしても時間が足りない。合理化した結果、単純な詰め込みになってしまう。
学校もカリキュラムに追われています。公立の学校もカリキュラムに追われています。塾も受験のカリキュラムに追われています。その結果、結局どちらもかたちは違えど、詰め込みをやってしまう。そうすると応用力・転用力が身についていかない。
さっきのは学校の例ですけど、中学受験でもほぼ同じことが起こっています。これは、中学受験の問題で非常によく出る定番問題ですね。

葉っぱ問題、ラグビーボール問題、唇問題、いろんな呼び方がされていますけれども、「この部分の面積を求めよ」。どうやって求めるか。ここに(正方形の対角線になるように)補助線を引くとわかりやすいんですよね。
補助線を引いて、扇型の面積を求めて、三角形の面積を引いて2倍する。あるいはこの図を展開して半円にしてしまって、大きい半円から大きい二等辺三角形を引くだけにするとかね。いろんな答え方はあると思います。
ところが、中学受験の多くの塾で、こんな教え方がされているんですよ。「この形が出てきたら正方形の面積に0.57を掛ける」「暗記して。0.57」「いくつ掛けるの? 0.57」。これ、「この形は全部正方形の面積の0.57倍が答えだな」と塾の先生が見つけてしまったんですね。だからそれを覚えさせる。
思考錯誤しながら補助線を引き、知っている知識を組み合わせることによって、解答を導き出すという脳の使い方を鍛えるためには、この算数の問題は非常に意味がありますよね。だけど、「この問題が出てきたら0.57」と言われて解けるようになっても、社会に出てから何の役にも立たないですよね。受験のために合理化したんですよ。
でも、本当に合理的ですか? 何かずれていませんか? そもそも何のために勉強しているのか。成長するためですよね。
目の前のテストで点数を取るためだったら、確かに0.57を掛けて計算を少なくしたほうが間違えないですよね。だけど本当にそれでいいんだろうか。そういう突っ込みを入れていかなければいけない。
ちなみに非常に算数ができる子は、上の解き方ができた上で0.57を覚えます。それなら問題ないですよね。ちゃんと補助線も引けますよ。でも時間が掛かってしまうので0.57を活用する。ところが問題はそうではなくて、算数が苦手な子です。
算数が苦手な子に、補助線の引き方を教えるのは非常に苦労する。なので先生たちも、苦手な子に限って0.57を暗記させるんですよ。そんなことをやっていたら、もともと算数が苦手なのに、もっと苦手になりますよ。でも中学受験という限られたゴールのために、それをやらざるを得なくなってしまっているといった問題点があるんだと思います。
続きを読むには会員登録
(無料)が必要です。
会員登録していただくと、すべての記事が制限なく閲覧でき、
スピーカーフォローや記事のブックマークなど、便利な機能がご利用いただけます。
すでに会員の方はこちらからログイン
名刺アプリ「Eight」をご利用中の方は
こちらを読み込むだけで、すぐに記事が読めます!
スマホで読み込んで
ログインまたは登録作業をスキップ
この記事をブックマークすると、同じログの新着記事をマイページでお知らせします