 PR
PR2024.12.10
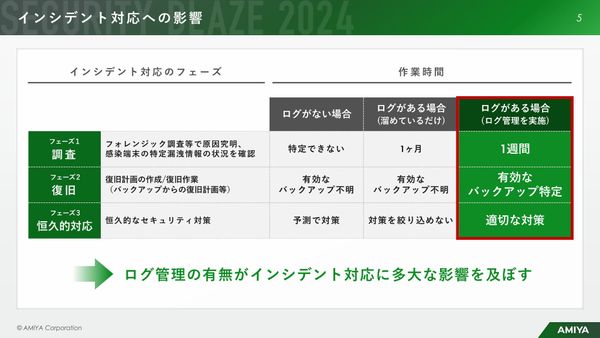
“放置系”なのにサイバー攻撃を監視・検知、「統合ログ管理ツール」とは 最先端のログ管理体制を実現する方法
How a Butterfly’s Wingbeat CAN Change the Weather(全1記事)
リンクをコピー
記事をブックマーク
「バタフライ・エフェクト」という言葉を聞いたことがあるでしょうか。蝶の羽ばたきが、不思議なことに竜巻を引き起こす原因になるというものです。
そんなことはありえませんよね。蝶はいつだって、世界中のどこででも羽ばたいているのですから、蝶の羽ばたきがすべての異常気象の原因では無いことは明らかです。
ところで、これは全くの誤りというわけではありません。蝶の羽ばたきは、思いがけない方法で気象に影響を与えているのです。
過去の些末な変化が未来に重大な結末を引き起こしてしまい、「ジョン・F・ケネディが生きている並行世界が存在してしまう」といった考えがバタフライ・エフェクトであると、一般には認識されているようです。
しかし、バタフライ・エフェクトをきちんと解説するには、コンピュータ時代の幕開けとなった近代科学を用いた気象予報、つまり気象学の黎明期である1960年代にまで遡る必要があります。
気象の変化は、気流や海流によって生じますね。こういった流動体を観測することで、そよ風から竜巻の発生に至るまで理由付けすることができます。しかし、このような気象をいざ予報するとなると、流体力学は複雑であるため非常に困難なのです。
流動体に適用される数式の煩雑さは悪名高く、その解はわかりづらく、複雑怪奇になりがちで、算出は困難です。そのため気象予報は、20世紀までは科学というよりは技能でした。
しかし、大学にコンピュータが導入された1960年代、研究者たちはこれらの数式の解を導き出し精緻な予報を得るために、すぐにコンピュータを取り入れました。そのとたん、数学と物理学を永遠に変えてしまいかねない壁にぶつかったのです。
気象や加速器などの物理システムのシミュレーションを行う場合には、時間経過によるシステムの変化の解析に適用される、微分方程式を用いる必要があります。その数式には、初期変数を入力します。つまり、必要な初期の数値を入力すると、時間経過後の状態が明示されるのです。
コンピュータを用いた手法を最初に導入した一人が、エドワード・ノートンです。ちょっと待ってください、エドワード・ノートンですって? いいえ、映画『ファイトクラブ』の主人公ではなく、アメリカの数学者にして気象学者のエドワード・ノートン・ローレンツですよ。
彼の不思議な発見は、1961年のある日、簡素化気象システムをシミュレーションしていた時に起こりました。同じ数式に同じ初期変数を導入しても、2つの異なる予報が導き出されたのです。何だかおかしな話ですよね。同じ初期変数、同じ数式を用いるのであれば、導き出される解は同じはずです。
入念に調べたところ、入力された初期値は、まったく同じ物ではないことがわかりました。ローレンツが片方の数式に入力したのは、0.506127の端数を切り捨てた0.506でした。彼はそれで差異が生じるとは思ってもみなかったのですが、実際は生じました。
しかも、2つの予報の差異は0.1パーセントにはとどまらず、シミュレーションの4日ごとに倍増し、1か月後には原型をとどめないほどの差異を生み出したのです。
結論は、初期の些末な変化が、大きく異なる結果に繋がる可能性があるというものでした。ローレンツはこのことを「ブラジルの蝶の羽ばたきは、テキサスの竜巻を引き起こすのか?」と題した講義で解説し、「バタフライ・エフェクト」という考えが誕生したのでした。
ローレンツは講義で、極論にならないよう配慮して「全ての竜巻は蝶が原因」「全ての蝶は竜巻を起こす」などとは言わず、些末なできごとが「竜巻を起こす一助となりうる」と語るにとどめました。
例えば、仮に2つのまったく同じ惑星があるとして、そのうち一方だけに蝶が1匹多くいるとすれば、片方の惑星には竜巻が発生し、もう片方には発生しないといった可能性は理論上はありえます。これがバタフライ・エフェクトの驚くべき真実なのです。
しかしローレンツの論は、どの蝶の羽ばたきが気候の変動に繋がるかを解明する術は無いと強く主張しています。たった1つの要因を解明するには、凄まじく精密なコンピュータでも無い限り、些末な要因が多すぎるのです。しかも、蝶が竜巻を防ぐ役を果たしている可能性もありえます。
こういった発見の数々から、数学の新しい分野が開拓されました。それが「カオス理論」です。カオス理論は、過去の些末な変化が未来に大きな影響を与え、初期条件に非常に敏感な、気象などのシステムに適用されます。
このような現象は多方面で見られるため、数学の新しい分野として認められるようになりました。土星の輪における重力相互作用や、二重振り子の揺れ、地球の地磁気の動きなどがその例です。
非常に不思議なことに、自然界はカオス状態に見えるにもかかわらず、これらのシステムには多くの共通点があることです。カオスには、どうやら普遍的な働きと構造が隠されているようなのです。
例えば、先に挙げた例の特性をグラフにしてみると、永遠に繰り返される不思議な幾何学模様である、フラクタルが多く見られるのです。
こういったことは、気象予報とはどのように関わってくるのでしょうか。まず、過去数十年で予報の精度が飛躍的に上がりました。気象衛星その他からのインプットデータの精度が上がり、コンピュータの性能が向上し、アルゴリズムが改良されたおかげで、より正確に、より長期間の気象現象の予報が可能になっています。カオス理論の研究が進んだことも大きな原因です。
とはいえ、数日後のことを予報しようとすると、それが何であれ、カオス理論が作り出す「戦場の霧」によって明瞭にはなりません。量子力学と同様に、物理法則は、人の未来予測に厳しく制限を敷いているかのようです。
大気の流れであれ、歴史の潮流であれ、私たちの身の周りはカオスに満ちており、これを究明するべく努力する価値は十分にあるのです。
関連タグ:

2024.12.10
メールのラリー回数でわかる「評価されない人」の特徴 職場での評価を下げる行動5選

2024.12.09
10点満点中7点の部下に言うべきこと 部下を育成できない上司の特徴トップ5

2024.12.09
国内の有名ホテルでは、マグロ丼がなんと1杯「24,000円」 「良いものをより安く」を追いすぎた日本にとって値上げが重要な理由

2023.03.21
民間宇宙開発で高まる「飛行機とロケットの衝突」の危機...どうやって回避する?

2024.12.10
職場であえて「不機嫌」を出したほうがいいタイプ NOと言えない人のための人間関係をラクにするヒント

2024.12.12
会議で発言しやすくなる「心理的安全性」を高めるには ファシリテーションがうまい人の3つの条件

2024.12.06
嫌いな相手の行動が気になって仕方ない… 臨床心理士が教える、人間関係のストレスを軽くする知恵

PR | 2024.11.26
なぜ電話営業はなくならない?その要因は「属人化」 通話内容をデータ化するZoomのクラウドサービス活用術

2024.12.11
大企業への転職前に感じた、「なんか違うかも」の違和感の正体 「親が喜ぶ」「モテそう」ではない、自分の判断基準を持つカギ

PR | 2024.11.22
「闇雲なAI導入」から脱却せよ Zoom・パーソル・THE GUILD幹部が語る、従業員と顧客体験を高めるAI戦略の要諦