スーパーでの買い物も「決定変数」になる
では「意思決定デザインを実際どのように進めるんだい?」という話になりますが、簡単なフレームワーク(FW)を作っています。最適化をやっている方にとってはあまり違和感のないものをフレームワークの形にしています。
FWの右上の象限には意思決定とアクションによって得たい価値を配置しています。価値に向かうためのアクション、つまり意思決定したい事象そのものは左下に、意思決定を取り巻くルールや前提条件は右下に、参照情報とかデータを左上に配置しています。
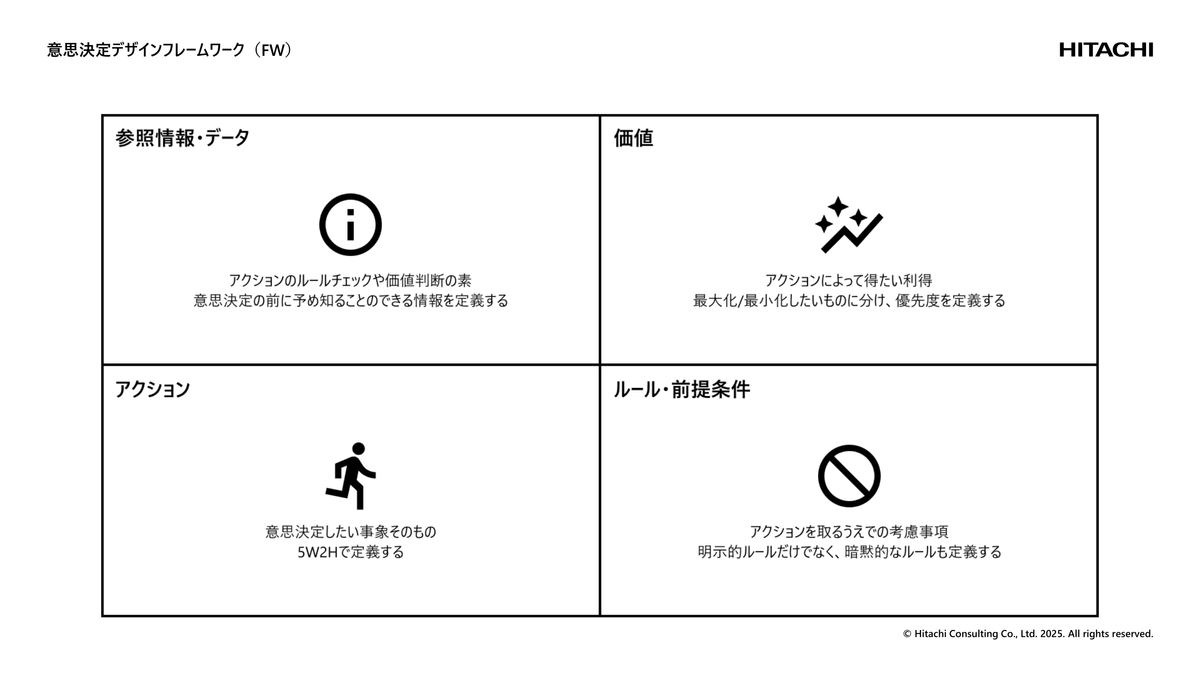
それらを最適化の用語にすると、価値は目的関数、アクションは決定変数、ルール・前提条件は制約、参照情報・データはインプットデータになりますが、これらを定義していくことが意思決定デザインだと僕は言っています。
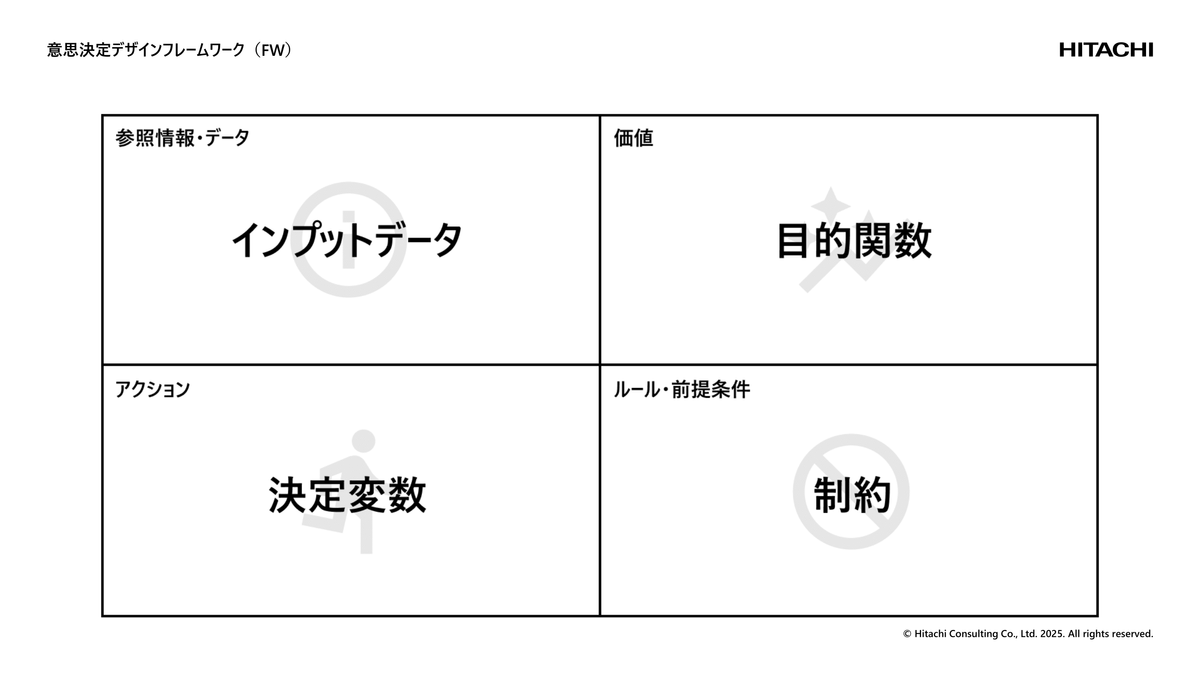
また、価値とアクションを「イシューの骨格」と、つまり「その問題の骨格になる部分だ」と言っていて、なぜかというと、意思決定者の内部に存在するエレメント、要素だと捉えているからです。

それに対して、ルールや前提条件、参照情報・データは輪郭と言っています。これは基本的には外部で規定される要素なのかなと考えて、種類分けをしています。これについては、後で少し話をしたいと思います。

じゃあ、どういう教え方をしているかというと、僕はよく会社で「日常に意思決定はあふれているよね」という話をするんですけど、その際に例として、僕はスパゲティのペペロンチーノが好きなので、「じゃあ、材料調達のためにスーパーに行ってください」と。「出入口からそれぞれの売り場で必要な材料を調達して、レジで会計を済ませて帰ってきてください」みたいな。「そうしたら、どういう形になるでしょうか?」みたいな話をしています。

そうなると、価値としてはなるべく最短距離で売り場を回りたいですよね。アクションは「どこから、どこへ、どの順番で」という、最適化を実際にやられている方からすると違和感があるかもしれないけど、こう考えています。
ルールや前提条件は、すべての材料を買って、レジを通って帰ってくるといったものになります。その時に必要な参照情報は、買い出しする材料のリスト、材料ごとの売り場と売り場同士の距離がわかると最短ルートを考えられそうですね。

次に、おうちに帰ってきました。どういう順番で調理したら早くスパゲティペペロンチーノを食べることができるかという問題になります。
この場合の価値は、作り始めから作り終わりまでの時間を短くすることになると思います。そうするとアクションは、どの作業をどの設備でいつ開始するか、になります。

ルールと前提条件がメチャクチャ多いんですけれども、全部の作業を行うであるとか、ジョブ同士の前後関係、つまりお湯を沸かしてからでないとスパゲティをゆでることはできないなどがありますよね。

さらに参照情報としては、レシピや調理手順、コンロは1つなのか2つなのかなどの調理設備構成、各作業の所要時間があります。社内で意思決定デザインの教育をする時は、「こんなものが必要になるんじゃないの?」という話をした上で、こうした日常の問題が実は最適化の問題であることに気づいてもらい、興味を持ってもらうようにしています。
初学者が最適化を身につける「守破離」アプローチ
ここからは、意思決定デザインのフレームワークを使いながら、お客さまとのコミュニケーションや教育をどう進めるかというお話をしていきたいと思います。
まずは、初学者の私がMIPモデリングをどうやって覚えていったかという話をします。日本には「守破離」という便利な言葉があるので、その概念を基に説明したいと思います。
私は本当に最初、何もわからなかったんですよ。最適化の概念も知らず、同僚のSさんという方が私にいろいろ教えてくれました。それがすごく自分の中で腹落ちしたので、今回はそれをベースにお話ししたいと思います。
最初わからない時は、まずは「守」のフェーズになります。ありがたいことにSさんがサンプルコードを書いてくれたので、まずそれを読み込んでわかるところ、わからないところをピックアップしました。
最初のハードルは0-1の決定変数の概念の理解でした。ここがSさんがすごくて、絵解きで理解させてくれたんですね。ここが自分にはとてもわかりやすくて、それ以降MIPの概念をよくすごく理解できるようになったんです。
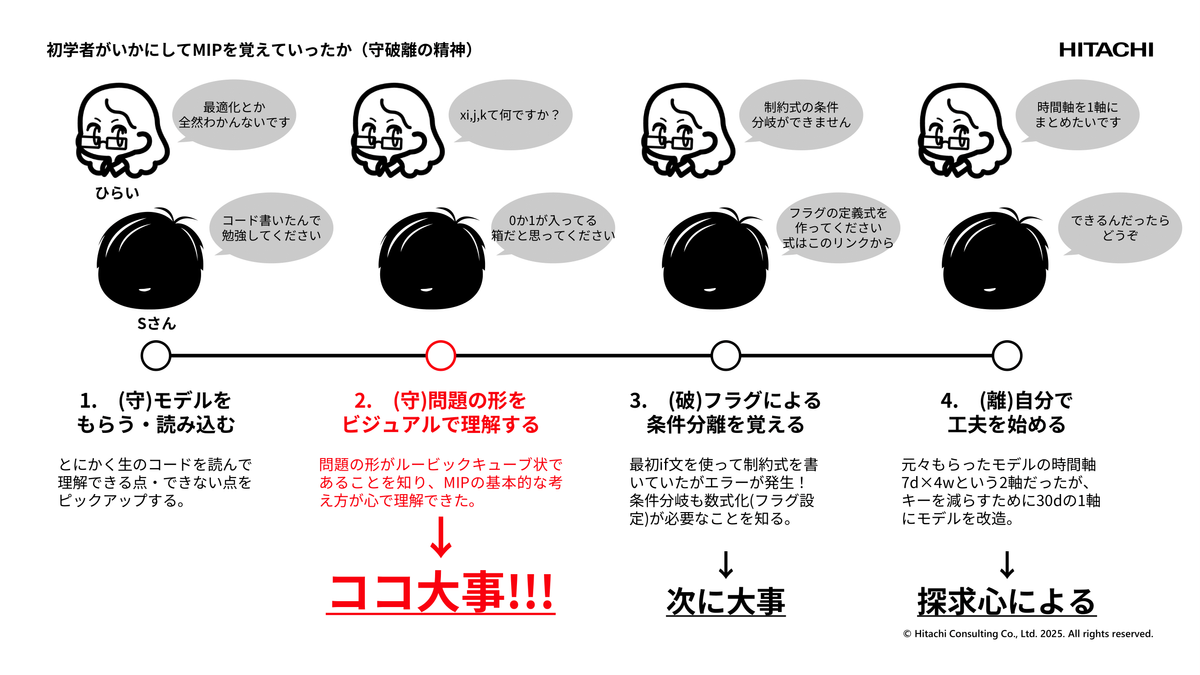
その後「離」のフェーズに入ります。私は最初のモデルに新しい制約を加えたくなったのですが、if文で制約を表現することができないということを知らなかったので、if文を使った制約で書いていたらエラーを吐いてしまいました。
Sさんに聞いてみると「それはできないんですよ」と言われて、「なのでif条件を表現するフラグ定義式を作ってください」と言われました。そこで、big-M法の概念や考え方を教えてもらいました。
このように、Sさんが最初教えてくれなかったこともいったん自分でやって相談を繰り返しながら少しずつモデルに改変を加えていきました。
最後に「離」のフェーズですが、ある程度慣れてきたところで、モデルそのものの形を変えたいと考えるようになって、「こういうモデルの形にしたいんですけど」とSさんに相談したら「できるならぜんぜんやっていいですよ」って言われたので、試すことにしました。
最終的にもらったモデルから形を変えて、自分独自のモデルを創る、つまり元のモデルから離れることができました。このような流れで私は学習しましたが、一番大事なのはやはりビジュアルで理解することなのかなと思っています。
0-1変数を「絵解き」で理解する
では、モデルのビジュアルイメージは自分の中ではどうなっているかというと、最初、「基本MIPベースで考えるから、0か1が入る箱が集まって出来上がっていると思ってください」と言われたんですよ。つまり、箱の一つひとつにYesかNo、つまり1か0かが入っているということです。
先ほどお話ししたペペロンチーノの材料調達の例では、「どこから、どこへ、どの順番で」という3次元の立体回転パズルのような問題の形になります。
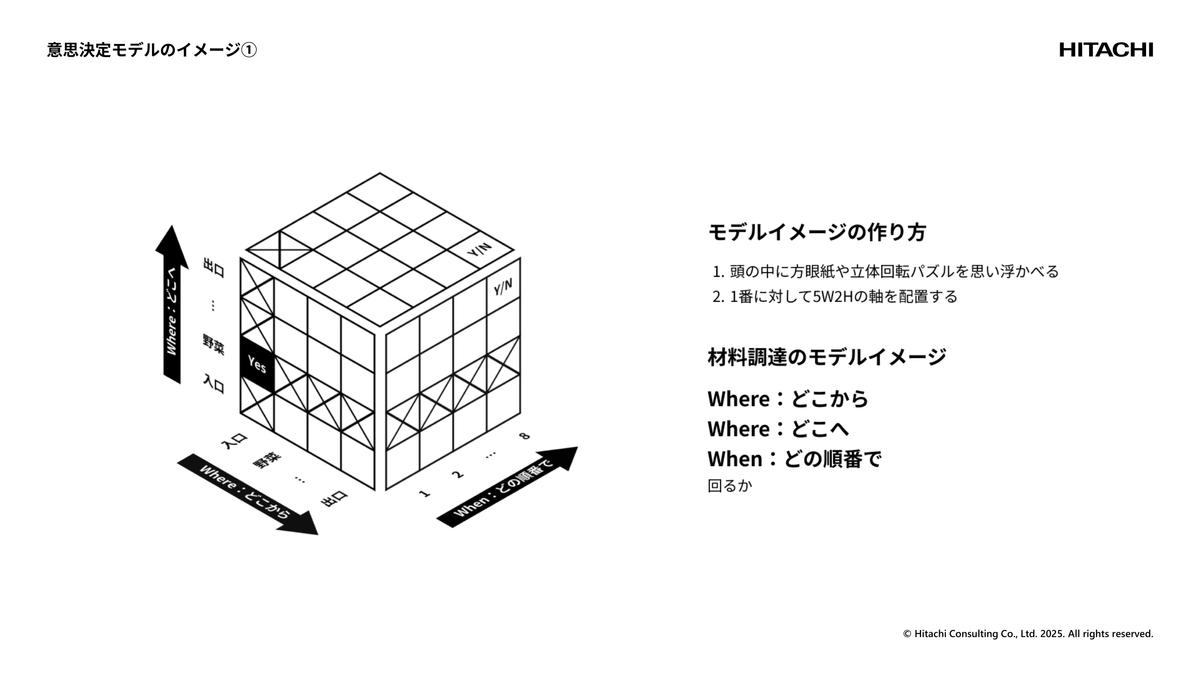
次はいわゆるone-hot制約の絵解きになります。最初に入り口から別の場所に行く場合を考えると、入り口から別の場所に向かう・向かわないという0-1の箱が束になっています。その0-1の箱同士を足し合わせた時の合計値が1になる、つまり0か1しかこの箱に入らないのだから、どれか1つに1が入れば他は絶対0になります。
だから右辺を1にすることで1つの選択肢が選ばれるようになる、とSさんから説明されて、ここで「あっ、そういうことなんだ」と私は納得したと同時にものすごく感動しました。それが契機になって、最適化テクノロジーそのものに対する理解や好奇心が強くなりました。

おそらく最適化の概念を持たない方にその概念を教える時って非常に苦労するかと思いますが、もしかしたらこういった絵解きで教えることで、うまくわかってもらえるんじゃないかと思っています。
次ですが、私も教育側に回ると「えっ、そこで引っかかるの?」みたいなこともあります。その最たる例がキーとバリューの話になります。
どういうことかというと、代数記法に慣れてない人は任意のキーのIDによって任意の値、バリューを呼び出すという考え方に慣れるのに時間がかかるということです。僕ももちろん、みんな代数記法に慣れていないわけですよ。
それをどうクリアしたか、あるメンバーに聞いたのですが、こうしました、みたいな話をされたんですね。
どういうことかというと、これは先ほどの材料調達を例にとると、地点間、売り場間の距離ですね。というのは、2つの場所によって定義される値なので「距離・地点・地点」という形で理解したということでした。最初から記号にしちゃうと、人によっては、もうそこで「ノーサンキュー」になっちゃうんで(笑)。
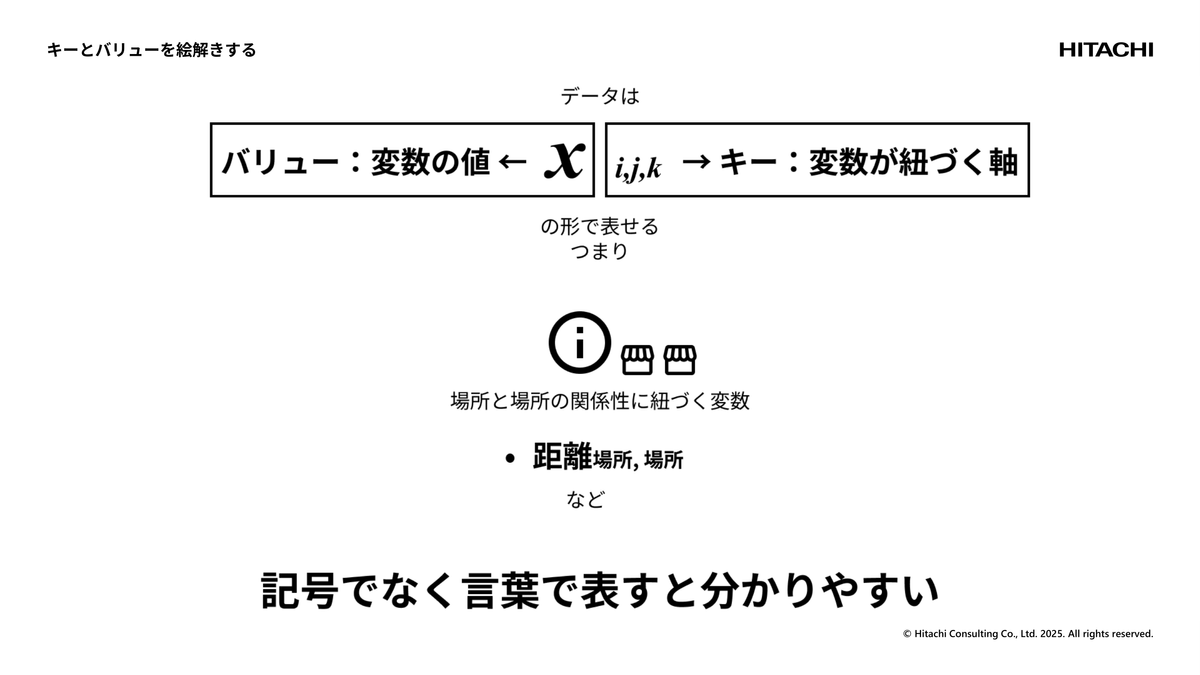
だから面倒でもその人たちが使う言葉に直して説明する、翻訳してあげる、そういう地道なことが効くようです。そのように翻訳した上で「こう考えたらわかる?」って言うと、「なるほど、そういうことなんですね」となって次に進めると感じています。
 PR
PR